Mathematische Beweise - Wie geht man da ran?
-
DarkDragon
- Beiträge: 6291
- Registriert: 29.08.2004 08:37
- Computerausstattung: Hoffentlich bald keine mehr
- Kontaktdaten:
Hallo,
Danke für die Antworten. Ich hab mir das schon fast gedacht, dass es da keinen allgemeinen Ansatz gibt.
Wenn ich euch jetzt das Beispiel nenne das ich hab, hab ich keins mehr zum Prüfen ob ich es nun verstanden habe.
Ich bin erst heute Abend Zuhause und werde dann oder morgen/übermorgen Versuchen das hier zu beweisen:
Ich hab mir dazu erstmal jeweils eine Quantorenformel aufgestellt für f injektiv, g injektiv und g o f injektiv.
Dann hab ich gemerkt, dass ich nicht weiterkomme.
Vielleicht finde ich heute Abend oder am Wochenende noch raus was ich falsch mache.
Ich glaube das lässt sich so beweisen wie der Kettenschluss durch Modus Ponens bewiesen werden kann (Hab ich allerdings auch noch nie gemacht).
Bitte posted erstmal keine Lösung, sondern sagt mir nach den ersten Versuchen erstmal ob ich richtig liege oder gebt mir kleine Anhaltspunkte wo ich dabei falsch liege.
Ich melde mich dann wieder. (Ich bitte den Doppelpost dann zu entschuldigen, ich will dann sicher gehen, dass man merkt, dass ich etwas neues dazugeschrieben hab)
Danke für die Antworten. Ich hab mir das schon fast gedacht, dass es da keinen allgemeinen Ansatz gibt.
Wenn ich euch jetzt das Beispiel nenne das ich hab, hab ich keins mehr zum Prüfen ob ich es nun verstanden habe.
Ich bin erst heute Abend Zuhause und werde dann oder morgen/übermorgen Versuchen das hier zu beweisen:
(das g o f ist g kringel f, kein ohh (Buchstabe), injektiv = linkseindeutig)f, g seien beliebige Funktionen. f : A -> B, g : B -> C
Bewiesen werden soll: Wenn f injektiv und g injektiv, dann gilt g o f injektiv.
Ich hab mir dazu erstmal jeweils eine Quantorenformel aufgestellt für f injektiv, g injektiv und g o f injektiv.
Dann hab ich gemerkt, dass ich nicht weiterkomme.
Vielleicht finde ich heute Abend oder am Wochenende noch raus was ich falsch mache.
Ich glaube das lässt sich so beweisen wie der Kettenschluss durch Modus Ponens bewiesen werden kann (Hab ich allerdings auch noch nie gemacht).
Bitte posted erstmal keine Lösung, sondern sagt mir nach den ersten Versuchen erstmal ob ich richtig liege oder gebt mir kleine Anhaltspunkte wo ich dabei falsch liege.
Ich melde mich dann wieder. (Ich bitte den Doppelpost dann zu entschuldigen, ich will dann sicher gehen, dass man merkt, dass ich etwas neues dazugeschrieben hab)
Angenommen es gäbe einen Algorithmus mit imaginärer Laufzeit O(i * n), dann gilt O((i * n)^2) = O(-1 * n^2) d.h. wenn man diesen Algorithmus verschachtelt ist er fertig, bevor er angefangen hat.
-
Kaeru Gaman
- Beiträge: 17389
- Registriert: 10.11.2004 03:22
> f, g seien beliebige Funktionen. f : A -> B, g : B -> C
> Bewiesen werden soll: Wenn f injektiv und g injektiv, dann gilt g o f injektiv.
g ○ f ist dann A -> C ?
... da würde ich sagen "sieht man doch".. aber wie man das beweisen soll... xD
shit, Mathe-Leistung ist einfach viel zu lange her...
MP sieht mir passend aus...
jedenfalls ist das das, was bei mir im Kopp abläuft damit "sieht man doch" rauskommt...
> Bewiesen werden soll: Wenn f injektiv und g injektiv, dann gilt g o f injektiv.
g ○ f ist dann A -> C ?
... da würde ich sagen "sieht man doch".. aber wie man das beweisen soll... xD
shit, Mathe-Leistung ist einfach viel zu lange her...
MP sieht mir passend aus...
jedenfalls ist das das, was bei mir im Kopp abläuft damit "sieht man doch" rauskommt...
Der Narr denkt er sei ein weiser Mann.
Der Weise weiß, dass er ein Narr ist.
Der Weise weiß, dass er ein Narr ist.
-
DarkDragon
- Beiträge: 6291
- Registriert: 29.08.2004 08:37
- Computerausstattung: Hoffentlich bald keine mehr
- Kontaktdaten:
g ○ f ist A -> C, jap.Kaeru Gaman hat geschrieben:> f, g seien beliebige Funktionen. f : A -> B, g : B -> C
> Bewiesen werden soll: Wenn f injektiv und g injektiv, dann gilt g o f injektiv.
g ○ f ist dann A -> C ?
... da würde ich sagen "sieht man doch".. aber wie man das beweisen soll... xD
Genau das "sieht man doch" würd ich auch sagen, aber beweisen könnte ich es nicht. Manchmal gibt es auch sachen, da sag ich dann allerdings nicht "sieht man doch" und kanns trotzdem nicht beweisen.
Angenommen es gäbe einen Algorithmus mit imaginärer Laufzeit O(i * n), dann gilt O((i * n)^2) = O(-1 * n^2) d.h. wenn man diesen Algorithmus verschachtelt ist er fertig, bevor er angefangen hat.
OK, keine Antwort, aber mal ein Bild.
So eine Skizze der Situation hilft bei Beweisen sehr gut.
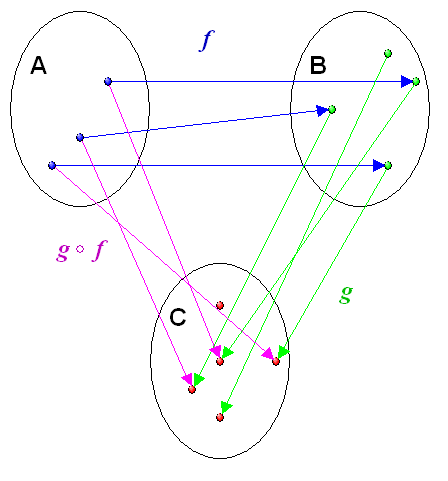
So eine Skizze der Situation hilft bei Beweisen sehr gut.
Zuletzt geändert von STARGÅTE am 10.07.2010 23:13, insgesamt 1-mal geändert.
PB 6.01 ― Win 10, 21H2 ― Ryzen 9 3900X, 32 GB ― NVIDIA GeForce RTX 3080 ― Vivaldi 6.0 ― www.unionbytes.de
Aktuelles Projekt: Lizard - Skriptsprache für symbolische Berechnungen und mehr
Aktuelles Projekt: Lizard - Skriptsprache für symbolische Berechnungen und mehr
hm...STARGÅTE hat geschrieben:Damit stünde er ja wieder vor einem Beweis, also das er eine Behauptung hat ... (die in dem falle dann das Gegenteil wäre) ... welche er Beweisen müsste, dass diese falsch ist, um den eigendliche Weg kommt er also nicht rum.
Beim direkten Beweis müßte man aber "alle Möglichkeiten" untersuchen, und wenn ich dann lese "das sieht man doch", verstehe ich wieder, was mein Pauker damals meinte.
Findet man beim indirekten Beweis keine richtige Lösung, ist die Ursprungsbehauptung richtig.
Ist das nicht einfacher als "hab ich denn an alle Möglichkeiten gedacht? ?
Das Problem wäre halt nur, für den indirekten Weg die richtige falsche Behauptung aufzustellen.
Ich bin blutiger PB-Anfänger.
seit 17.12.08: PB 4.3 unter XP Home(SP3)
seit 17.12.08: PB 4.3 unter XP Home(SP3)
OK,
Das geht aber nur bei solchen Beispielen gut:
Behauptung: Alle Zahlen sind Gerade.
Beweis : Wenn es eine zahl gibt die nicht gerade ist, gilt also die Behauptung nicht.
1 ist nicht gerade, also ist die Behauptung falsch.
Aber anders ist es wenn man nur eine "kleine" Sachen beweisen muss, denn dann müsste mal es für alle andere Dinge Widerlegen. Und dnan ist der Indirekte Beweise länger.
Und bei Tutor würde bei dem Satz sagen: "Findet man beim indirekten Beweis keine richtige Lösung, ist die Ursprungsbehauptung richtig",
"Dann ist man einfach zu blöd richtig zu rechnen und eine Lösung zu finden."
@ AUFGABE VON DD
Hier mal meine Lösung, DD nicht anklicken ^^
Das geht aber nur bei solchen Beispielen gut:
Behauptung: Alle Zahlen sind Gerade.
Beweis : Wenn es eine zahl gibt die nicht gerade ist, gilt also die Behauptung nicht.
1 ist nicht gerade, also ist die Behauptung falsch.
Aber anders ist es wenn man nur eine "kleine" Sachen beweisen muss, denn dann müsste mal es für alle andere Dinge Widerlegen. Und dnan ist der Indirekte Beweise länger.
Und bei Tutor würde bei dem Satz sagen: "Findet man beim indirekten Beweis keine richtige Lösung, ist die Ursprungsbehauptung richtig",
"Dann ist man einfach zu blöd richtig zu rechnen und eine Lösung zu finden."
@ AUFGABE VON DD
Hier mal meine Lösung, DD nicht anklicken ^^
Zuletzt geändert von STARGÅTE am 10.07.2010 23:13, insgesamt 1-mal geändert.
PB 6.01 ― Win 10, 21H2 ― Ryzen 9 3900X, 32 GB ― NVIDIA GeForce RTX 3080 ― Vivaldi 6.0 ― www.unionbytes.de
Aktuelles Projekt: Lizard - Skriptsprache für symbolische Berechnungen und mehr
Aktuelles Projekt: Lizard - Skriptsprache für symbolische Berechnungen und mehr
-
Kaeru Gaman
- Beiträge: 17389
- Registriert: 10.11.2004 03:22
>> Findet man beim indirekten Beweis keine ... Lösung
... hat man nicht alle Faktoren in Betracht gezogen.
das problem beim indirekten Beweis ist, dass er nur greift, wenn man ein unumstößliches Beispiel findet.
wenn man nichts findet, kann man auch keine Schlußfolgerung ziehen.
> DD nicht anklicken
 ...und suche uns nicht in der Unterführung!
...und suche uns nicht in der Unterführung! 
... hat man nicht alle Faktoren in Betracht gezogen.
das problem beim indirekten Beweis ist, dass er nur greift, wenn man ein unumstößliches Beispiel findet.
wenn man nichts findet, kann man auch keine Schlußfolgerung ziehen.
> DD nicht anklicken
Der Narr denkt er sei ein weiser Mann.
Der Weise weiß, dass er ein Narr ist.
Der Weise weiß, dass er ein Narr ist.
-
DarkDragon
- Beiträge: 6291
- Registriert: 29.08.2004 08:37
- Computerausstattung: Hoffentlich bald keine mehr
- Kontaktdaten:
Ohh mann ich weiß nicht ob ich so schnell dazukomm das zu machen. Hab grad wieder tonnenweise Übungen bekommen, sodass ich keine Zeit mehr zum Üben hab.
Darin ist grad fast genau so ein Beweis drin. Nur muss man "ist injektiv" mit "ist eine Funktion" (rechtseindeutig und linkstotal) ersetzen. In Informationsmanagement/Datenbanken würde man sagen A -> B, B ist funktional abhängig von A, also ist B praktisch eine imaginäre Teilmenge von A, das klingt ja auch logisch. Und wenn C eine imaginäre Teilmenge von B ist, ist C auch eine imaginäre Teilmenge von A. Denn C kann durch A bestimmt werden.
Darin ist grad fast genau so ein Beweis drin. Nur muss man "ist injektiv" mit "ist eine Funktion" (rechtseindeutig und linkstotal) ersetzen. In Informationsmanagement/Datenbanken würde man sagen A -> B, B ist funktional abhängig von A, also ist B praktisch eine imaginäre Teilmenge von A, das klingt ja auch logisch. Und wenn C eine imaginäre Teilmenge von B ist, ist C auch eine imaginäre Teilmenge von A. Denn C kann durch A bestimmt werden.
Angenommen es gäbe einen Algorithmus mit imaginärer Laufzeit O(i * n), dann gilt O((i * n)^2) = O(-1 * n^2) d.h. wenn man diesen Algorithmus verschachtelt ist er fertig, bevor er angefangen hat.
-
Kaeru Gaman
- Beiträge: 17389
- Registriert: 10.11.2004 03:22