Entretiens d'embauche chez Google

[Fig]

Question 1:

Comment trouver le premier caractère en double dans une chaîne de caractère ?

Par exemple dans cette chaine, le premier caractère en double est le (pas le A) mais le D !! (merci Marc)
Chaine$="POABCDEFTHLGDSALKL"

Il y a évidemment deux solutions, une naïve (qui vous vient déjà à l'esprit, ne niez pas ! ) en O(n²) et une plus efficace en O(n).
Jouez honnêtement le jeu, vous avez 30 secondes pour y réfléchir...


Du coup, on se dit qu'on devrait postuler, non ?

[Guillot]

Code : Tout sélectionner

Chaine$="POABCDEFTHLGDSALKL"

Dim c(255)
For i=1 To Len(Chaine$)
  a=Asc(Mid(chaine$,i,1))
  c(a)+1
  If c(a)=2:Debug Chr(a):End:EndIf
Next

[Fig]

Embauché !

[Guillot]

connaissent pas mes prétentions salariales !!

[Ollivier]

Pour aller plus vite :
http://www.purebasic.fr/french/viewtopi ... =6&t=16276
Il y a les SSE mais j'ai ommis où j'ai mis ça. C'est dans la section ASM. Ipistri ou Champistri, je sais plus...

And... Yea ! When Google becomes nake, Google becomes my friend ! A poil mon pote ! Rock n Roll !

Au fait... Mais... A qui profite le criiiii....
.....
...
(votre correspond s'est pris la comète "Tagoul 937" et c'est bien dommage pour lui, prends-en de la graine!)
...

[Marc56]

Comment trouver le premier caractère en double dans une chaîne de caractère ?
Par exemple dans cette chaine, le premier caractère en double est le A
Chaine$="POABCDEFTHLGDSALKL"

Ça dépend comment on perçoit le premier du double.
D'après le programme de Guillot et la logique pure, c'est D et pas A
P O A B C D E F T H L G D S A L K L



Voilà ma version (Code moche première fois que j'utilise une map)

Code : Tout sélectionner

Chaine$="POABCDEFTHLGDSALKL"
Debug "Chaine à traiter: " + Chaine$
NewMap Lettre.s()

For i = 1 To Len(Chaine$)
     Caratere.s = Mid(Chaine$, i, 1)
     Debug "#" + RSet(Str(i), 2, " ") + " -> " + Caratere
     If FindMapElement(Lettre(), Caratere)
          Debug "------ " + Caratere + " existe déjà !"
     Else
          AddMapElement(Lettre(), Mid(Chaine$, i, 1), #PB_Map_NoElementCheck)
     EndIf
Next

Code : Tout sélectionner

Chaine à traiter: POABCDEFTHLGDSALKL
# 1 -> P
# 2 -> O
# 3 -> A
# 4 -> B
# 5 -> C
# 6 -> D
# 7 -> E
# 8 -> F
# 9 -> T
#10 -> H
#11 -> L
#12 -> G
#13 -> D
------ D existe déjà !
#14 -> S
#15 -> A
------ A existe déjà !
#16 -> L
------ L existe déjà !
#17 -> K
#18 -> L
------ L existe déjà !

Mais c'est une méthode linéaire: le référentiel se construit au fur et à mesure.
Si la liste de référence est déjà construite, alors c'est effectivement le A qui sera vu en premier.
(mais j'ai toujours été nul en math, c'est pourquoi je n'ai pas compris le O(n²) et O(n) qui expriment sans doute cela d'une manière abstraite ?)

[GallyHC]

Bonjour,

Une autre version possible :

Code : Tout sélectionner

EnableExplicit

Define.l i
Define.s temp, char = "POABCDEFTHLGDSALKL"

For i=1 To Len(char) - 1
  temp = Mid(char, i, 1)
  If FindString(char, temp, i + 1) > 0
    Debug temp
    Break  
  EndIf
Next i

Cordialement,
GallyHC

[Ar-S]

Un peu plus de lignes..

Code : Tout sélectionner

Global NewList lettre.s()

Global char.s = "POABCDEFTHLGDSALKL"

For i=1 To Len(char) - 1 :   AddElement (lettre()) :   lettre() = Mid(char, i, 1) : Next i
SortList(Lettre(), #PB_Sort_Ascending)

For i=0 To Len(char) - 3
  SelectElement(lettre(),i)
  car1.s = lettre()
  SelectElement(lettre(),i+1)
  car2.s = lettre()
  If car1 = car2 : compte +1 : Debug "1er double trouvé : "+car1 : Break : EndIf
Next

[Fig]

Marc, tu as raison dans mon exemple c'est la lettre D qui est attendu et non le A comme je l'avais écrit.

Concernant la notation "Big O", ce n'est pas très compliqué mais fondamentale pour l'analyse de la vitesse des algorithmes indépendamment de l'implémentation.

http://bigocheatsheet.com/

Par exemple si tu dois examiner chaque élément d'une liste pour trouver la réponse à un problème, ton algo est de type O(n) cad que plus il y a d'éléments dans la liste (n éléments) plus ça sera proportionnellement long. C'est une droite.
Si pour chaque élément de la liste tu dois le comparer à chacun des autres éléments de cette même liste, tu fera n² itérations (soit une double boucle imbriquée). Dans ce cas, la courbe est quadratique au nombre d’éléments de la liste O(n²).
Cherche un élément en mémoire prend en moyenne un temps constant donc O(1)
Etc...
Selon le type d’algorithme et selon le nombre d’éléments traités, le but est de trouver un algo qui est calculable en un temps raisonnable.

Quelques exemples, en abscisse le nombre d'éléments, en ordonnée, le temps de traitement.


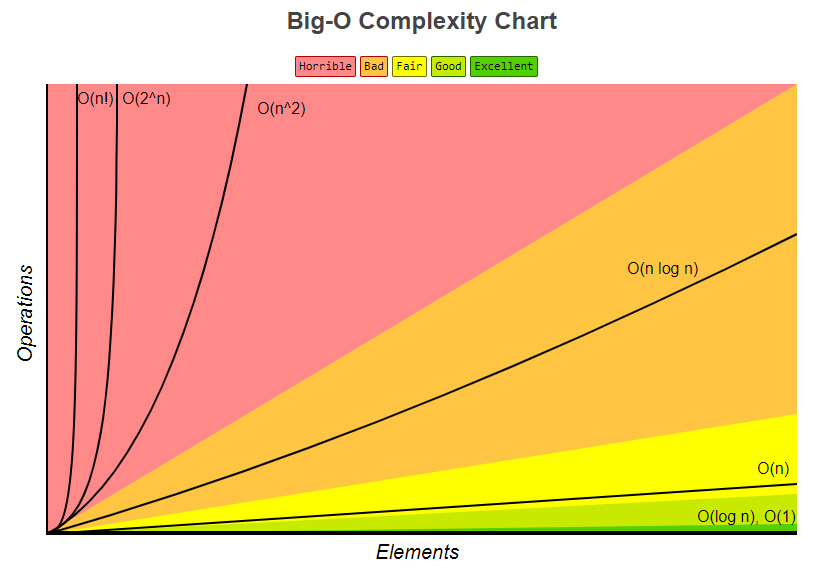
La réponse de GallyHC est O(n²) car chaque élément est comparé à tous les autres (la fonction findstring est une boucle en fait), la tienne O(n).
Celle de Ars qui utilise le tri des listes est O(n log n) -pour simplifier, mais en fait pire à cause des deux autres boucles-, en effet, le tri des listes chainées en Pb est un tri par fusion (il me semble).

Si il y a une complexité forte, ça reste acceptable dans la mesure où on traite peu d'éléments.

[Ar-S]

Ah du coup j'avais mal lu l'énoncé, mon code trouve les premières lettre en double mais pas celles qui apparaissent dans la liste en 1er

[Marc56]

Et dire que j'ai fais ça sans rien y comprendre
Je me suis simplement dit que comme les Maps refusent les doublons, il suffit de remplir avec chaque caractère et d'attendre le message d'erreur
(j'ai honte de ma logique cheap de vieux codeur autodidacte )

[nico]

Code de Gally modifié pour prendre en compte le premier doublon tel qu'on l'attend:

Code : Tout sélectionner

EnableExplicit

Define.l i, position, mem=65535
Define.s temp, first, char = "POABCDEFTHLGDSALKL"

For i=1 To Len(char) - 1
    temp = Mid(char, i, 1)
    position = FindString(char, temp, i + 1)
    If position > 0
        Debug temp
        If position<mem
            mem=position
            first = temp
        EndIf
    EndIf 
Next i

Debug "-----------------------------"
Debug mem
Debug first

[SPH]

Ma contribution :

Code : Tout sélectionner

chaine$="POABCDEFTHLGDSALKL"

Dim c.b(90)

For i=1 To Len(chaine$)
  c(Asc(Mid(chaine$,i,1)))+1
  If c(Asc(Mid(chaine$,i,1)))>1
    Debug Mid(chaine$,i,1)
    End
  EndIf
Next

Aucune idee du temps qu'elle met...

[GallyHC]

La version de Nico simplifié ^^ (pour le première version, j'avais surement mal compris) :

Code : Tout sélectionner

EnableExplicit

Define.s temp, char = "POABCDEFTHLGDSALKL"
Define.l i, lpos, lmem = Len(char)

For i=1 To Len(char) - 1
  temp = Mid(char, i, 1)
  lpos = FindString(char, temp, i + 1)
  If lpos > 0 And lpos < lmem
    lmem = lpos
  EndIf
Next i
If lmem > 0
  Debug Mid(char, lmem, 1)
EndIf

Cordialement,
GallyHC

[Torp]

Non c'est pas le D c'est la A

Code : Tout sélectionner

Chaine$="POABCDEFTHLGDSALKL"
For i = 1 To Len(Chaine$)
	txt$ = Mid(Chaine$, i, 1)
	a.a = CountString(Chaine$, txt$)
	If a= 2 : Debug txt$ : End : EndIf
Next i