Quick And Simple Bezier Curve Drawing

[Danilo]

From the Book Graphics Gems 5, Edited by Alan W. Paeth,
Chapter IV.8: 'Quick And Simple Bezier Curve Drawing' by Robert D. Miller

The Include contains 4 Procedures for calculating Bezier Curve coordinates from Point arrays.

For 2D: BezierForm2D() and BezierCurve2D()
For 3D: BezierForm3D() and BezierCurve3D()

Those procedures work on Arrays of type BezierPOINTF2D / BezierPOINTF3D.
I included 4 Macros for Array creation:

For 2D: PtArray2D(name,size) and BezArray2D(name,size)
For 3D: PtArray3D(name,size) and BezArray3D(name,size)

The procedures do not draw the curve, they are only for calculating the points.

I included some procedures for drawing in the examples: DrawBezierCurve(), DrawBezierCurveArray(), DrawBezierText()





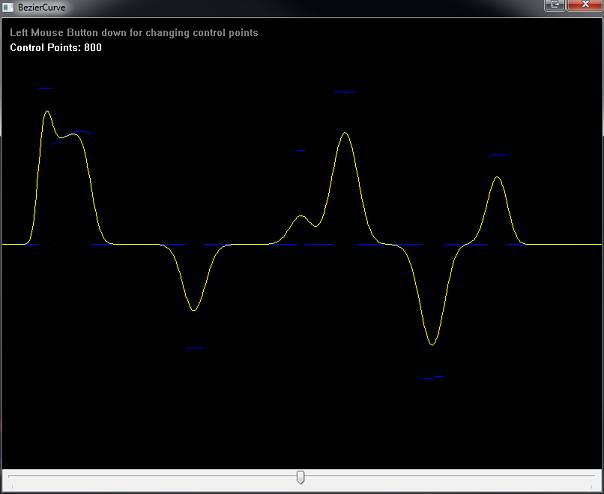
How to use the procedures?

First you create an array with your points for the bezier curve:

Code: Select all

    PtArray2D(pn,4)

    pn(0)\x = x1  : pn(0)\y = y1
    pn(1)\x = x2  : pn(1)\y = y2
    pn(2)\x = x3  : pn(2)\y = y3
    pn(3)\x = x4  : pn(3)\y = y4

x1,y1 etc. are your screen coordinates.

Now you call BezierForm2D with your point array and a second array that gets initialized:

Code: Select all

    BezArray2D(bc,4)

    BezierForm2D(4,pn(),bc())

The array bc() contains now the initialized values for your curve.

Now you call the procedure BezierCurve2D() with your bc() array to get a point on the curve:

Code: Select all

BezierCurve2D(NumPointsInArray, bc() , *pt.BezierPOINTF2D, t.d)

t.d specifies the point on the curve you want to get. t.d has to be between 0.0 and 1.0.

The requested coordinate is now in *pt\x and *pt\y (and *pt\z for the 3D version).

To get all points from start to end, use a loop:

Code: Select all

    For k = 0 To stepSize
        BezierCurve2D(4,bc(),@pt, k/(stepSize*1.0))

        ; coordinate is now in *pt\x and *pt\y (and *pt\z for the 3D version)
    Next k

The bigger the stepSize, the more points you get. Logical, it is a For..Next loop.

You control the interpolation with the stepSize. If you use a small stepSize like 5,
you get only 6 points and if you draw lines between the points, it is most likely not
a nice curve.
If you use a higher stepSize like 50, you get 51 interpolated points... and your curve
looks smoother.

The following two images show the same control points with low and high stepSize:




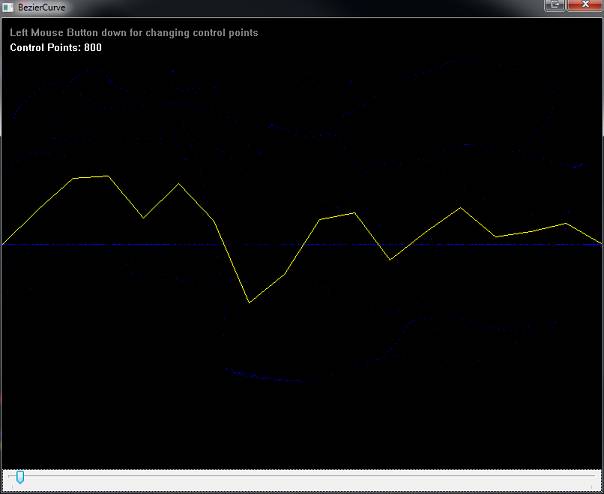
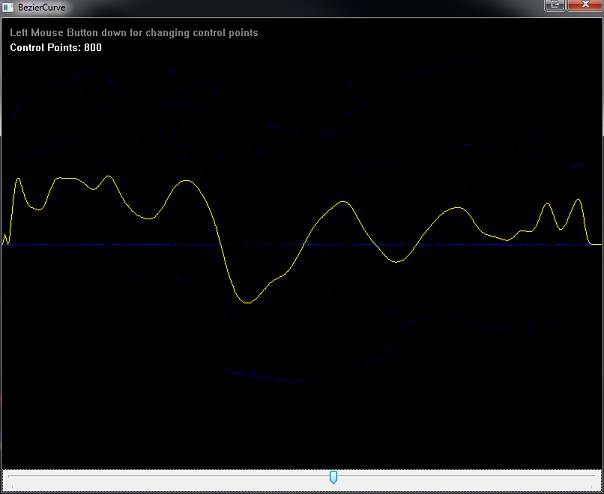
All 4 included examples contain a TrackBar on the bottom to control the stepSize.
Move the TrackBar to the start and you get less points.


DOWNLOAD: BezierCurve.zip (5.5k)
(contains the Include and examples)


The include BezierCurve.pbi:

Code: Select all

;
; Graphics Gems 5, Edited by Alan W. Paeth
;
; http://www.amazon.com/Graphics-Version-Morgan-Kaufmann-Computer/dp/0125434553/
;
; Chapter IV.8  -  Quick And Simple Bezier Curve Drawing
;
; By Robert D. Miller
;

;
; 2D version
;
Structure BezierPOINTF2D
    x.d
    y.d
EndStructure


Macro PtArray2D(_var_,_size_)
   Dim _var_.BezierPOINTF2D(_size_)
EndMacro

Macro BezArray2D(_var_,_size_)
    Dim _var_.BezierPOINTF2D(_size_)
EndMacro


Procedure BezierForm2D(NumCtlPoints, Array p.BezierPOINTF2D(1), Array c.BezierPOINTF2D(1))
    ;
    ; Setup Bezier coefficient array once for each control polygon
    ;
    Protected  k, choose.d
    Protected.i n = NumCtlPoints-1
    
    For k = 0 To n

        If     k = 0 : choose = 1
        ElseIf k = 1 : choose = n
        Else         : choose = choose * (n-k+1)/(k*1.0)
        EndIf
        
        c(k)\x = p(k)\x * choose
        c(k)\y = p(k)\y * choose

    Next k
EndProcedure


Procedure BezierCurve2D(NumCtlPoints, Array c.BezierPOINTF2D(1), *pt.BezierPOINTF2D, t.d)
    ;
    ; Return *pt.BezierPOINTF2D, t <= 0 <= 1,
    ; given the number of Points in control polygon,
    ; BezierForm2D must be called once for any given control polygon
    ;
    Protected.i k, n
    Protected.d t1, tt, u
    
    BezArray2D(b,NumCtlPoints)

    n = NumCtlPoints - 1
    u = t
    
    b(0)\x = c(0)\x
    b(0)\y = c(0)\y

    For k = 1 To n

        b(k)\x = c(k)\x * u
        b(k)\y = c(k)\y * u
    
        u = u * t

    Next k

    *pt\x = b(n)\x
    *pt\y = b(n)\y
    t1    = 1-t
    tt    = t1
    
    k = n-1
    While k >= 0

        *pt\x + ( b(k)\x * tt )
        *pt\y + ( b(k)\y * tt )
    
        tt = tt * t1
        
        k-1
    Wend
EndProcedure



;
; 3D version
;
Structure BezierPOINTF3D
    x.d
    y.d
    z.d
EndStructure


Macro PtArray3D(_var_,_size_)
    Dim _var_.BezierPOINTF3D(_size_)
EndMacro

Macro BezArray3D(_var_,_size_)
    Dim _var_.BezierPOINTF3D(_size_)
EndMacro

Procedure BezierForm3D(NumCtlPoints, Array p.BezierPOINTF3D(1), Array c.BezierPOINTF3D(1))
    ;
    ; Setup Bezier coefficient array once for each control polygon
    ;
    Protected  k, choose.d
    Protected.i n = NumCtlPoints-1
    
    For k = 0 To n

        If     k = 0 : choose = 1
        ElseIf k = 1 : choose = n
        Else         : choose = choose * (n-k+1)/(k*1.0)
        EndIf
        
        c(k)\x = p(k)\x * choose
        c(k)\y = p(k)\y * choose
        c(k)\z = p(k)\z * choose ; use for 3D curves

    Next k
EndProcedure

Procedure BezierCurve3D(NumCtlPoints, Array c.BezierPOINTF3D(1), *pt.BezierPOINTF3D, t.d)
    ;
    ; Return *pt.BezierPOINTF3D, t <= 0 <= 1,
    ; given the number of Points in control polygon,
    ; BezierForm3D must be called once for any given control polygon
    ;
    Protected.i k, n
    Protected.d t1, tt, u
    
    BezArray3D(b,NumCtlPoints)

    n = NumCtlPoints - 1
    u = t
    
    b(0)\x = c(0)\x
    b(0)\y = c(0)\y
    b(0)\z = c(0)\z  ; for 3D curves

    For k = 1 To n

        b(k)\x = c(k)\x * u
        b(k)\y = c(k)\y * u
        b(k)\z = c(k)\z * u  ; for 3D curves
    
        u = u * t

    Next k

    *pt\x = b(n)\x
    *pt\y = b(n)\y
    t1    = 1-t
    tt    = t1
    
    k = n-1
    While k >= 0

        *pt\x + ( b(k)\x * tt )
        *pt\y + ( b(k)\y * tt )
        *pt\z + ( b(k)\z * tt )  ; again, 3D
    
        tt = tt * t1
        
        k-1
    Wend
EndProcedure


;---------------------------------------------------------------------------

[Danilo]

The possible control points (array-size) were limited to round about 122 because it used floats for calculations.

- Changed the include to use doubles
- Changed example 3 to show 10 control points only
- Added example 4 with 800 control points

Please download again if you already downloaded: BezierCurve.zip (5.5k)
(contains the Include and examples)

[srod]

Nice work Danilo. Nice code.

[blueb]

Testing Example_04... If I get a little wild with the left mouse button
and 'exceed' the edges... the EXE crashes and I get a compiler error.

Win7 Pro 64 PB 4.61b2 x86

PS. Nice samples Danilo

[Foz]

Damn you're good. And a mind reader as well! I was just about to do a search for Bezier Curves implemented in PB!

This makes my life so much easier

Do you mind writing my next project for me before I even know what I want written ?

[Danilo]

Thanks for the comments guys!

Testing Example_04... If I get a little wild with the left mouse button
and 'exceed' the edges... the EXE crashes and I get a compiler error.

Yes, I've seen that too. So i added a small check and the CanvasGadget flag #PB_Canvas_ClipMouse.
Didn't crash anymore here, but it is simple examples only.

Updated Example 4:

Code: Select all

EnableExplicit

XIncludeFile "BezierCurve.pbi"

Procedure DrawBezierCurveArray(Array pn.BezierPOINTF2D(1), stepSize.f, color.q=-1)
    Protected.BezierPOINTF2D pt, oldPt
    Protected k
    Protected numPoints = ArraySize(pn())

    BezArray2D(bc,numPoints)

    BezierForm2D(numPoints,pn(),bc())

    For k = 0 To stepSize

        BezierCurve2D(numPoints,bc(),@pt, k/(stepSize*1.0))
        
        If k = 0
            oldPt = pt
        Else
            If color = -1 : LineXY(oldPt\x,oldPt\y,pt\x,pt\y)
            Else          : LineXY(oldPt\x,oldPt\y,pt\x,pt\y,color)
            EndIf
            oldPt = pt
        EndIf

    Next k

EndProcedure

Global PtArray2D(pn,800)
Global i

For i = 0 To 799
    pn(i)\x = i
    pn(i)\y = 300 ;+ Sin(i*0.1)*200 ;+Random(300)
Next i

Procedure Draw(steps)
    If StartDrawing(CanvasOutput(0))
        Box(0,0,800,600,0)

        ;pn(000)\x = 000 : pn(000)\y = 300
        ;pn(799)\x = 800 : pn(799)\y = 300

        For i = 0 To 799
            Plot(pn(i)\x,pn(i)\y,RGB($00,$00,$FF))
        Next i
     
        DrawBezierCurveArray(pn(),steps,RGB($FF,$FF,$00))

        DrawingMode(#PB_2DDrawing_Transparent)
        DrawText(10,10,"Left Mouse Button down for changing control points",RGB($80,$80,$80))
        DrawText(10,30,"Control Points: "+Str(ArraySize(pn())))
        DrawText(10,50,"Bezier Curve Steps: "+Str(steps))

        StopDrawing()
    EndIf
EndProcedure

OpenWindow(0,0,0,800,630,"BezierCurve",#PB_Window_ScreenCentered|#PB_Window_SystemMenu)
CanvasGadget(0,0,0,800,600,#PB_Canvas_ClipMouse)
TrackBarGadget(1,0,600,800,30,3,1000) : SetGadgetState(1,500)

Draw(500)

Repeat
    Select WaitWindowEvent()
        Case #PB_Event_CloseWindow
            End
        Case #PB_Event_Gadget
            If EventGadget()=0
                If EventType()=#PB_EventType_LeftClick Or EventType()=#PB_EventType_MouseMove
                    If GetGadgetAttribute(0,#PB_Canvas_Buttons)=#PB_Canvas_LeftButton
                        Define x = GetGadgetAttribute(0,#PB_Canvas_MouseX)
                        Define y = GetGadgetAttribute(0,#PB_Canvas_MouseY)
                        ;Debug x
                        ;Debug y
                        If x >= 0 And x <= 800 And y >= 0 And y <= 600
                            pn(x)\y = y
                            Draw( GetGadgetState(1) )
                        EndIf
                    EndIf
                EndIf
            ElseIf EventGadget()=1
                Draw( GetGadgetState(1) )
            EndIf
    EndSelect
ForEver

BTW: Did somebody test it on Linux and MacOS? Should be platform independent, except Example1: "LoadFont(0,"Arial",14)" (but should still run)

[Guimauve]

BTW: Did somebody test it on Linux and MacOS? Should be platform independent, except Example1: "LoadFont(0,"Arial",14)" (but should still run)

Tested on LinuxMint 12 x64 and PureBasic 4.61B2, no problem with all 4 examples.

Best regards
Guimauve

[Michael Vogel]

I've simplified the code for interpolating recorded data points which works fine, if less than 1024 points are given. Otherwise, the scaling factor will get infinitive.elow Any idea, how to change the whole thing to be sure to allow 5.000 or even 500.000 data points?

To see the problem, change the BezierCount value to 1023.

Code: Select all

; Define

	EnableExplicit

	Structure BezierPoint
		x.d
		y.d
	EndStructure

	#BezierDots=200
	#BezierNull=0.001
	#BezierX=50
	#BezierY=50
	#BezierW=500
	#BezierH=300
	#BezierMark=4
	#BezierAlphaMark=$80000000
	#BezierAlphaText=$C0000000

	#BezierColorFill=$FDE1D0
	#BezierColorMark=$FCCAAB
	#BezierColorLine=$FA9151

	Global BezierCount=1000;   works until set to values higher than 1022
	Global BezierLen
	Global BezierMax
	Global BezierMin

	Global Dim BezierInit.BezierPoint(BezierCount)

; EndDefine
Procedure BezierDraw()

	Protected i,k,lines
	Protected choose.d,t.d,t1.d,t2.d,u.d
	Protected Dim BezierDots.BezierPoint(BezierCount)
	Protected Dim BezierTemp.BezierPoint(BezierCount)
	Protected BezierDraw.BezierPoint
	Protected BezierLast.BezierPoint

	lines=BezierCount-1

	For k=0 To lines
		If k=0
			choose=1
		ElseIf k=1
			choose=lines
		Else
			choose=choose*(lines-k+1)/k
		EndIf
		BezierDots(k)\x=BezierInit(k)\x*choose
		BezierDots(k)\y=BezierInit(k)\y*choose
		
		If k>lines*0.45 And k<lines*0.52
			Debug Str(k)+": "+StrD(BezierDots(k)\x)
		EndIf
	Next k


	For i=0 To #BezierDots
		t.d=i/#BezierDots
		u=t
		BezierTemp(0)\x=BezierDots(0)\x
		BezierInit(i)\y=i-Sin(i/50)*100+Random(100)

		For k=1 To lines
			BezierTemp(k)\x=BezierDots(k)\x*u
			BezierTemp(k)\y=BezierDots(k)\y*u
			u*t
		Next k

		BezierDraw\x=BezierTemp(lines)\x
		BezierDraw\y=BezierTemp(lines)\y
		t1=1-t
		t2=t1

		k=lines-1
		While k>=0
			BezierDraw\x+BezierTemp(k)\x*t2
			BezierDraw\y+BezierTemp(k)\y*t2
			t2*t1
			k-1
		Wend

		If i
			LineXY(#BezierX+BezierLast\x,#BezierY+BezierLast\y,#BezierX+BezierDraw\x,#BezierY+BezierDraw\y,#BezierColorLine)
			BezierLast=BezierDraw
		Else
			BezierLast=BezierDraw
		EndIf

	Next i

EndProcedure
Procedure Draw()

	Protected i,n,k
	Protected s.s
	Protected z.f,scale.f
	
	BezierMin=99999
	BezierMax=-9999

	For i=0 To BezierCount
		BezierInit(i)\x=i
		BezierInit(i)\y=i
		If BezierInit(i)\y>BezierMax
			BezierMax=BezierInit(i)\y
		EndIf
		If BezierInit(i)\y<BezierMin
			BezierMin=BezierInit(i)\y
		EndIf
	Next i

	BezierLen=BezierInit(BezierCount)\x

	If BezierMin>0
		BezierMin=0
	EndIf
	If BezierMax-BezierMin>#Null
		scale=#BezierH/(BezierMax-BezierMin)
	Else
		scale=0
	EndIf
	For i=0 To BezierCount
		BezierInit(i)\y=(BezierInit(i)\y-BezierMin)*scale
	Next i

	scale=(#BezierW-1)/BezierLen
	For i=0 To BezierCount
		BezierInit(i)\x=BezierInit(i)\x*scale
	Next i

	StartDrawing(CanvasOutput(0))

	Box(0,0,800,600,#White)
	DrawingMode(#PB_2DDrawing_Default)
	BezierDraw()
	DrawingMode(#PB_2DDrawing_Outlined)
	Box(#BezierX,#BezierY,#BezierW,#BezierH,#BezierColorLine)

	StopDrawing()

EndProcedure

OpenWindow(0,0,0,600,400,"BezierCurve",#PB_Window_ScreenCentered|#PB_Window_SystemMenu)
CanvasGadget(0,0,0,600,400,#PB_Canvas_ClipMouse)

Draw()

Repeat
	Select WaitWindowEvent()
	Case #PB_Event_CloseWindow
		End
	EndSelect
ForEver