Was sind Matrizen?
Ich hab da mal ein paar Fragen:
1.) Was kann ich mit Matrizen alles ausrechnen? Ist das eine Art Gleichungs-Lösungs-System?
2.) Was sind komplexe Zahlen? Reelle Zahlen kann man nicht mehr mit einer Gleichung lösen. Was für Zahlen beiben dann noch übrig?
Ich hoffe es kann mir jemand weiterhelfen...
Danke, Andreas
1.) Was kann ich mit Matrizen alles ausrechnen? Ist das eine Art Gleichungs-Lösungs-System?
2.) Was sind komplexe Zahlen? Reelle Zahlen kann man nicht mehr mit einer Gleichung lösen. Was für Zahlen beiben dann noch übrig?
Ich hoffe es kann mir jemand weiterhelfen...
Danke, Andreas
du hast da jetzt ne menge durch einander geworfen^^
1.
eine Matrix ist die mathematische Form eine Abbildung,
eine Abbildung nimmt Zahlen und bearbeitet sich und schmeißt sie wieder raus:
Beispiel: Du möchtest einen 2D-Vektor (x,y) um drehen, dann kannst du das in mehreren Schritten machen oder den Vektor in diese Matrix werfen:
und bekommst dann einen neuen Vektor der um den Winkel gedreht ist.
Und ja du kannst es auch als Gleichguns system verwenden:
1*x1+3*x2 = 7
2*x1+0*x2 = 2
Ergebnis wäre also x1 = 1, x2 = 2
2.
Komplexe Zahlen sind eine weitere Erweiterung der Zahlenmengen.
Für die Gleichung x²+1 = 0 gibt es in der Menge der Reellen Zahlen keine Lösung.
Also hat man gesagt, man definiert x²+1 = 0 hat eine lösung im Komplexen, nämlich i und -i.
i ist somit Definiert als i²=-1
"Reelle Zahlen kann man nicht mehr mit einer Gleichung lösen"
Wieso nicht ?
x²=2
dann ist x = √2
und √2 ist reel
du meinst sicher das man reele Zahlen nicht als Bruch darstellen kann was man ja bei den Rationalen kann
1.
eine Matrix ist die mathematische Form eine Abbildung,
eine Abbildung nimmt Zahlen und bearbeitet sich und schmeißt sie wieder raus:
Beispiel: Du möchtest einen 2D-Vektor (x,y) um drehen, dann kannst du das in mehreren Schritten machen oder den Vektor in diese Matrix werfen:
Code: Alles auswählen
┌ ┐ ┌ ┐
│ Cos(Winkel) -Sin(Winkel) │ │ x │
│ Sin(Winkel) Cos(Winkel) │ │ y │
└ ┘ └ ┘
Und ja du kannst es auch als Gleichguns system verwenden:
1*x1+3*x2 = 7
2*x1+0*x2 = 2
Code: Alles auswählen
┌ ┬ ┐
│ 1 3 │ 7 │
│ 2 0 │ 2 │
└ ┴ ┘
┌ ┬ ┐
│ 1 3 │ 7 │
│ 0 -6 │-12 │
└ ┴ ┘
┌ ┬ ┐
│ 1 3 │ 7 │
│ 0 1 │ 2 │
└ ┴ ┘
┌ ┬ ┐
│ 1 0 │ 1 │
│ 0 1 │ 6 │
└ ┴ ┘
2.
Komplexe Zahlen sind eine weitere Erweiterung der Zahlenmengen.
Für die Gleichung x²+1 = 0 gibt es in der Menge der Reellen Zahlen keine Lösung.
Also hat man gesagt, man definiert x²+1 = 0 hat eine lösung im Komplexen, nämlich i und -i.
i ist somit Definiert als i²=-1
"Reelle Zahlen kann man nicht mehr mit einer Gleichung lösen"
Wieso nicht ?
x²=2
dann ist x = √2
und √2 ist reel
du meinst sicher das man reele Zahlen nicht als Bruch darstellen kann was man ja bei den Rationalen kann
Zuletzt geändert von STARGÅTE am 17.01.2008 15:38, insgesamt 2-mal geändert.
PB 6.01 ― Win 10, 21H2 ― Ryzen 9 3900X, 32 GB ― NVIDIA GeForce RTX 3080 ― Vivaldi 6.0 ― www.unionbytes.de
Aktuelles Projekt: Lizard - Skriptsprache für symbolische Berechnungen und mehr
Aktuelles Projekt: Lizard - Skriptsprache für symbolische Berechnungen und mehr
Danke für die rasche Antwort und gute Erklärung!
1. Oh... das ist eine nette Funktion...
Hoffe das ich das auch im 3 Dimensionalen schaffe^^
2. Gibt es nicht auch Zahlen die man nichtmal mehr mit einer Gleichung darstellen kann? Ich glaub Irrational...
PI zB kann man ja nicht mehr in einer Gleichung ausdrücken, wenn ich mich nicht irre.
Danke nochmal!
Andreas
1. Oh... das ist eine nette Funktion...
Hoffe das ich das auch im 3 Dimensionalen schaffe^^
2. Gibt es nicht auch Zahlen die man nichtmal mehr mit einer Gleichung darstellen kann? Ich glaub Irrational...
PI zB kann man ja nicht mehr in einer Gleichung ausdrücken, wenn ich mich nicht irre.
Danke nochmal!
Andreas
klar kann man PI mit einer Gleichung beschreiben, man braucht nur "bessere" Mathematik:
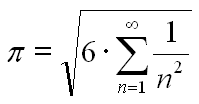
damit kannst du PI so genau berechnen wie du willst, kannst du ja mal in PB schrieben ^^
damit kannst du PI so genau berechnen wie du willst, kannst du ja mal in PB schrieben ^^
;Berechung von PI
Repeat
Delay(1)
n + 1
Wert.d + 1/(n*n)
PI.d = Sqr(Wert*6)
Debug "n="+Str(n)+" PI="+StrD(PI)
ForEver
Zuletzt geändert von STARGÅTE am 09.07.2010 14:37, insgesamt 1-mal geändert.
PB 6.01 ― Win 10, 21H2 ― Ryzen 9 3900X, 32 GB ― NVIDIA GeForce RTX 3080 ― Vivaldi 6.0 ― www.unionbytes.de
Aktuelles Projekt: Lizard - Skriptsprache für symbolische Berechnungen und mehr
Aktuelles Projekt: Lizard - Skriptsprache für symbolische Berechnungen und mehr
Im prinzip ja, aber es scheitert ja schon an der "Unendlichen" Summe die da unter der Wurzel steht.also breuchte man nur eine Wurzel Funktion die Unendlich genau ist
du musst ja:
1/1+1/4+1/9+1/16+1/25+1/36......
rechnen und das bis ins unendliche.
PB 6.01 ― Win 10, 21H2 ― Ryzen 9 3900X, 32 GB ― NVIDIA GeForce RTX 3080 ― Vivaldi 6.0 ― www.unionbytes.de
Aktuelles Projekt: Lizard - Skriptsprache für symbolische Berechnungen und mehr
Aktuelles Projekt: Lizard - Skriptsprache für symbolische Berechnungen und mehr
- NicTheQuick
- Ein Admin
- Beiträge: 8835
- Registriert: 29.08.2004 20:20
- Computerausstattung: Ryzen 7 5800X, 64 GB DDR4-3200
Ubuntu 24.04.2 LTS
GeForce RTX 3080 Ti - Wohnort: Saarbrücken
Zufällig ist ATan() nichts anderes als eine unendliche Summe:

Unendlich, auch wenn am Schluss nur noch winzige Teilchen dazu addiert
werden.

Da hast du Recht. Aber würde das Quadrat da nicht stehen, wäre die SummeAndreas_S hat geschrieben:Ja da hast du recht... aber wenn dann irgendwann 1/(1000000^2) steht dann ist das ja auch nur noch ein winziges teilchen in den hintersten stellen...
Unendlich, auch wenn am Schluss nur noch winzige Teilchen dazu addiert
werden.
Zuletzt geändert von NicTheQuick am 17.01.2008 18:08, insgesamt 1-mal geändert.
- Froggerprogger
- Badmin
- Beiträge: 855
- Registriert: 08.09.2004 20:02
Zu Matrix siehe auch hier: http://de.wikipedia.org/wiki/Matrix_%28Mathematik%29
und zu komplexen Zahlen: http://de.wikipedia.org/wiki/Komplexe_Zahl
Wikipedia ist gerade bei mathematischen Themen sehr gut. Meistens findet sich dort eine einfach geschriebene Einführung und zum Ende hin gibt es zunehmend mehr Details, bis hin zu Uni-Niveau.
und zu komplexen Zahlen: http://de.wikipedia.org/wiki/Komplexe_Zahl
Wikipedia ist gerade bei mathematischen Themen sehr gut. Meistens findet sich dort eine einfach geschriebene Einführung und zum Ende hin gibt es zunehmend mehr Details, bis hin zu Uni-Niveau.
!UD2