PureBasic

; la suite de Fibonacci est représenté dans toute choses de la nature , c'est la suite de "Dieu"
; par exemple , on retrouve dans cette liste , le nombre de spirale d'un tournesol, d'un Ananas ,d'une pomme de pin etc..
; le nombre de pétales de toutes les variété de fleurs ....(ou presque)
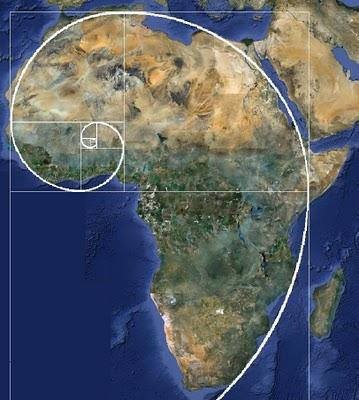
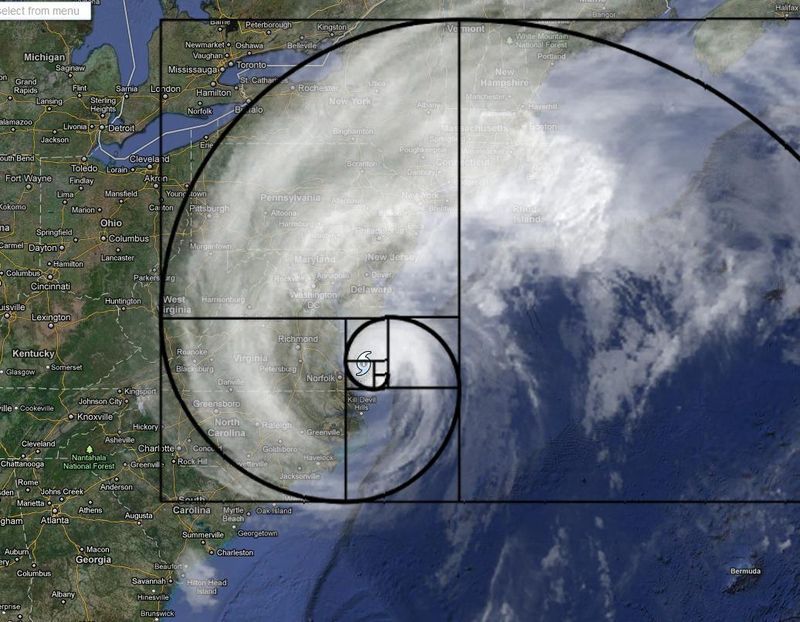
; la spirale dessinée a l'aide de la suite de Fibonacci , se retrouve dans la nature, par exemple nombre de coquillages ont cette particularités
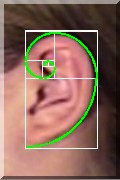
; la forme de nos oreilles est un debut de spirale calqué sur la spirale de Fibonacci etc ......
; si l'on fait un rectangle en utilisant les nombres de la suite de Fibonacci ex un rectangle qui ferait 21cm x 13 cm , il serai de proportion parfaite on dit
; qu'il s'agit d'un Rectangle d'or !
; si on divise 2 termes qui se suivent , de la suite de Fibonacci , par exemple 21/13 = on arrive a approcher le chiffre de 1.618 qui est considéré comme le nombre d'or
; cette proportion , ce rapport (1.618) se retrouve dans toutes choses sur terre ,
; par exemple :
; plus on se rapproche de cette proportion, plus la chose observé est "Parfaite"
; exemple un visage parfait (un beau visage ) , aura la largeur du Nez 1.618 fois plus petit que la largeur de la bouche
; la hauteur entre la base du menton et de la bouche sera environs 1.618 fois plus petite que la hauteur entre la base du nez ,et la base du menton,
; la largeur de la bouche et la largeur du visage, largeur des deux yeux et largeur de bouche
; longueur du bras, et longueur de l'avant bras, longueur du fémur et longueur du tibia etc ..

; les sections de nos doigts représentent aussi cette proportion ... la premiere parti d'un doigt qui va de la main a la premiere articulation est environs 1.618 fois plus grande que
; la partie qui va de la premiere articulation a la deuxiemme ...
; la taille de notre Majeur est environ 1.618 fois plus grande que la taille de l'auriculaire .....
; la largeur de nos dents etc ....

; je pourrai continuer comme ça longtemps


; ce qui fait dire a certaines personne, que c'est la preuve que notre monde ,n'est pas un hasard !

Et c'est tellement vrai, en plus.

J'ose pas esayer de calculer ma tronche.. j'ai peur du résultat
Surement un calcul difficile à faire, en fait un nombre "d'or dur" quoi

d'autres exemple de la suite de fibonacci et de sa correspondance avec notre monde

apres ça, peut t'on encore parler de hasard concernant notre création ?







<---- LOL on peut rire hein ?




pour finir : une petit video qui tue :

https://www.youtube.com/watch?v=v5TaiKC7QuA

Donald Fibronacci Trump Exellent !
Le cyclone parfait est pas mal non plus... En fait le monde est bel et bien mathématiquement construit... Autant certains pensent que c'est une théorie fumeuse (comme ca l'est pour le 666 et les biorythmes qu'on a déja vu sur le forum, et auquel je ne crois pas (du tout)), mais pour moi, cet agencement mathématique des choses est bien réel, il n'y a qu'a regarder, c'est troublant tellement ca concorde... Par contre de là à l'expliquer... ca reste un mystére.
En tout cas merci pour ce petit cours Dobro
"Tous les jours, découvrez un fait incroyable expliqué par le célébre Docteur Professeur Dobro "

Donald Trump !
Très fort
C'est vrai que ça fait partie des mystères de l'univers, sur lesquels notre malheureuse espèce bien limitée, se cassera les dents encore longtemps. Peut-être même qu'elle se fera rattraper au petit jeu de l'évolution par d'autres espèces à l'esprit plus géométrique (escargots ?).
Peut-être aussi que ces singularités sont liées à l'existence de l'univers lui-même, et qu'il ne sert à rien de courir après, ou après quoi que ce soit d'ailleurs...

Et ce qu'on voit à notre échelle, existe surement d'en d'autres.