Quick And Simple Bezier Curve Drawing
Posted: Sun Apr 29, 2012 1:27 pm
From the Book Graphics Gems 5, Edited by Alan W. Paeth,
Chapter IV.8: 'Quick And Simple Bezier Curve Drawing' by Robert D. Miller
The Include contains 4 Procedures for calculating Bezier Curve coordinates from Point arrays.
For 2D: BezierForm2D() and BezierCurve2D()
For 3D: BezierForm3D() and BezierCurve3D()
Those procedures work on Arrays of type BezierPOINTF2D / BezierPOINTF3D.
I included 4 Macros for Array creation:
For 2D: PtArray2D(name,size) and BezArray2D(name,size)
For 3D: PtArray3D(name,size) and BezArray3D(name,size)
The procedures do not draw the curve, they are only for calculating the points.
I included some procedures for drawing in the examples: DrawBezierCurve(), DrawBezierCurveArray(), DrawBezierText()




How to use the procedures?
First you create an array with your points for the bezier curve:
x1,y1 etc. are your screen coordinates.
Now you call BezierForm2D with your point array and a second array that gets initialized:
The array bc() contains now the initialized values for your curve.
Now you call the procedure BezierCurve2D() with your bc() array to get a point on the curve:
t.d specifies the point on the curve you want to get. t.d has to be between 0.0 and 1.0.
The requested coordinate is now in *pt\x and *pt\y (and *pt\z for the 3D version).
To get all points from start to end, use a loop:
The bigger the stepSize, the more points you get. Logical, it is a For..Next loop. 
You control the interpolation with the stepSize. If you use a small stepSize like 5,
you get only 6 points and if you draw lines between the points, it is most likely not
a nice curve.
If you use a higher stepSize like 50, you get 51 interpolated points... and your curve
looks smoother.
The following two images show the same control points with low and high stepSize:
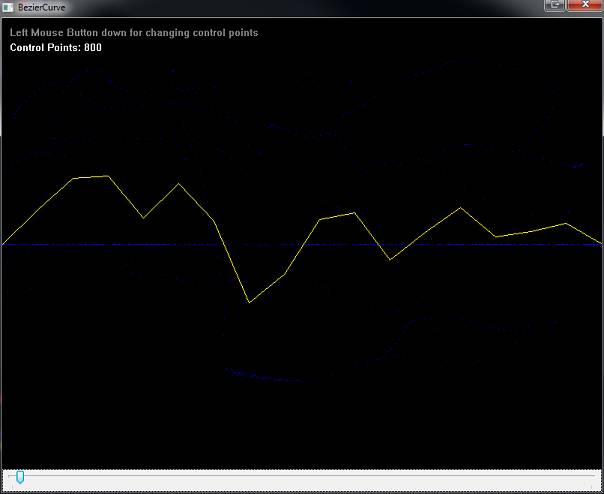
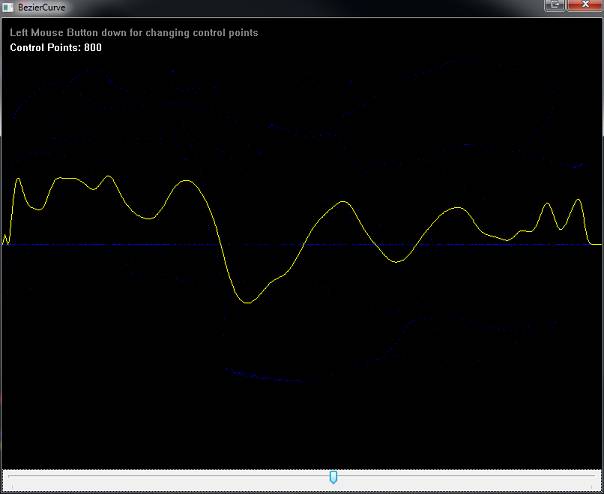
All 4 included examples contain a TrackBar on the bottom to control the stepSize.
Move the TrackBar to the start and you get less points.
DOWNLOAD: BezierCurve.zip (5.5k)
(contains the Include and examples)
The include BezierCurve.pbi:
Chapter IV.8: 'Quick And Simple Bezier Curve Drawing' by Robert D. Miller
The Include contains 4 Procedures for calculating Bezier Curve coordinates from Point arrays.
For 2D: BezierForm2D() and BezierCurve2D()
For 3D: BezierForm3D() and BezierCurve3D()
Those procedures work on Arrays of type BezierPOINTF2D / BezierPOINTF3D.
I included 4 Macros for Array creation:
For 2D: PtArray2D(name,size) and BezArray2D(name,size)
For 3D: PtArray3D(name,size) and BezArray3D(name,size)
The procedures do not draw the curve, they are only for calculating the points.
I included some procedures for drawing in the examples: DrawBezierCurve(), DrawBezierCurveArray(), DrawBezierText()




How to use the procedures?
First you create an array with your points for the bezier curve:
Code: Select all
PtArray2D(pn,4)
pn(0)\x = x1 : pn(0)\y = y1
pn(1)\x = x2 : pn(1)\y = y2
pn(2)\x = x3 : pn(2)\y = y3
pn(3)\x = x4 : pn(3)\y = y4Now you call BezierForm2D with your point array and a second array that gets initialized:
Code: Select all
BezArray2D(bc,4)
BezierForm2D(4,pn(),bc())
Now you call the procedure BezierCurve2D() with your bc() array to get a point on the curve:
Code: Select all
BezierCurve2D(NumPointsInArray, bc() , *pt.BezierPOINTF2D, t.d)The requested coordinate is now in *pt\x and *pt\y (and *pt\z for the 3D version).
To get all points from start to end, use a loop:
Code: Select all
For k = 0 To stepSize
BezierCurve2D(4,bc(),@pt, k/(stepSize*1.0))
; coordinate is now in *pt\x and *pt\y (and *pt\z for the 3D version)
Next kYou control the interpolation with the stepSize. If you use a small stepSize like 5,
you get only 6 points and if you draw lines between the points, it is most likely not
a nice curve.
If you use a higher stepSize like 50, you get 51 interpolated points... and your curve
looks smoother.
The following two images show the same control points with low and high stepSize:


All 4 included examples contain a TrackBar on the bottom to control the stepSize.
Move the TrackBar to the start and you get less points.
DOWNLOAD: BezierCurve.zip (5.5k)
(contains the Include and examples)
The include BezierCurve.pbi:
Code: Select all
;
; Graphics Gems 5, Edited by Alan W. Paeth
;
; http://www.amazon.com/Graphics-Version-Morgan-Kaufmann-Computer/dp/0125434553/
;
; Chapter IV.8 - Quick And Simple Bezier Curve Drawing
;
; By Robert D. Miller
;
;
; 2D version
;
Structure BezierPOINTF2D
x.d
y.d
EndStructure
Macro PtArray2D(_var_,_size_)
Dim _var_.BezierPOINTF2D(_size_)
EndMacro
Macro BezArray2D(_var_,_size_)
Dim _var_.BezierPOINTF2D(_size_)
EndMacro
Procedure BezierForm2D(NumCtlPoints, Array p.BezierPOINTF2D(1), Array c.BezierPOINTF2D(1))
;
; Setup Bezier coefficient array once for each control polygon
;
Protected k, choose.d
Protected.i n = NumCtlPoints-1
For k = 0 To n
If k = 0 : choose = 1
ElseIf k = 1 : choose = n
Else : choose = choose * (n-k+1)/(k*1.0)
EndIf
c(k)\x = p(k)\x * choose
c(k)\y = p(k)\y * choose
Next k
EndProcedure
Procedure BezierCurve2D(NumCtlPoints, Array c.BezierPOINTF2D(1), *pt.BezierPOINTF2D, t.d)
;
; Return *pt.BezierPOINTF2D, t <= 0 <= 1,
; given the number of Points in control polygon,
; BezierForm2D must be called once for any given control polygon
;
Protected.i k, n
Protected.d t1, tt, u
BezArray2D(b,NumCtlPoints)
n = NumCtlPoints - 1
u = t
b(0)\x = c(0)\x
b(0)\y = c(0)\y
For k = 1 To n
b(k)\x = c(k)\x * u
b(k)\y = c(k)\y * u
u = u * t
Next k
*pt\x = b(n)\x
*pt\y = b(n)\y
t1 = 1-t
tt = t1
k = n-1
While k >= 0
*pt\x + ( b(k)\x * tt )
*pt\y + ( b(k)\y * tt )
tt = tt * t1
k-1
Wend
EndProcedure
;
; 3D version
;
Structure BezierPOINTF3D
x.d
y.d
z.d
EndStructure
Macro PtArray3D(_var_,_size_)
Dim _var_.BezierPOINTF3D(_size_)
EndMacro
Macro BezArray3D(_var_,_size_)
Dim _var_.BezierPOINTF3D(_size_)
EndMacro
Procedure BezierForm3D(NumCtlPoints, Array p.BezierPOINTF3D(1), Array c.BezierPOINTF3D(1))
;
; Setup Bezier coefficient array once for each control polygon
;
Protected k, choose.d
Protected.i n = NumCtlPoints-1
For k = 0 To n
If k = 0 : choose = 1
ElseIf k = 1 : choose = n
Else : choose = choose * (n-k+1)/(k*1.0)
EndIf
c(k)\x = p(k)\x * choose
c(k)\y = p(k)\y * choose
c(k)\z = p(k)\z * choose ; use for 3D curves
Next k
EndProcedure
Procedure BezierCurve3D(NumCtlPoints, Array c.BezierPOINTF3D(1), *pt.BezierPOINTF3D, t.d)
;
; Return *pt.BezierPOINTF3D, t <= 0 <= 1,
; given the number of Points in control polygon,
; BezierForm3D must be called once for any given control polygon
;
Protected.i k, n
Protected.d t1, tt, u
BezArray3D(b,NumCtlPoints)
n = NumCtlPoints - 1
u = t
b(0)\x = c(0)\x
b(0)\y = c(0)\y
b(0)\z = c(0)\z ; for 3D curves
For k = 1 To n
b(k)\x = c(k)\x * u
b(k)\y = c(k)\y * u
b(k)\z = c(k)\z * u ; for 3D curves
u = u * t
Next k
*pt\x = b(n)\x
*pt\y = b(n)\y
t1 = 1-t
tt = t1
k = n-1
While k >= 0
*pt\x + ( b(k)\x * tt )
*pt\y + ( b(k)\y * tt )
*pt\z + ( b(k)\z * tt ) ; again, 3D
tt = tt * t1
k-1
Wend
EndProcedure
;---------------------------------------------------------------------------