Re: Any maths gurus who can help with geometry?!
Posted: Fri Jan 22, 2010 12:08 am
Hello,
Here is a code. You can use mouse wheel and drag the two blue points in the screen to check if it's good. You can check the flag box's at the top-left corner.
I didn't change more the code because it consists now in merging all the procedures. So, you couldn't understand easily the operations.
Thank to Michel Berteau site and particularly this page which allows me to create quickly the CircleEquation() procedure. (Note that there is small errors in the calculs at the end of the page, but I think it's willingly for the school cheaters to be betrayed if they copy foolishly. I don't think the author's wrong.)
@Seymour Clufley
You forgot a detail we can see here. In the global inventory, we need some flags the explanation could be well illustrated below (from official page).
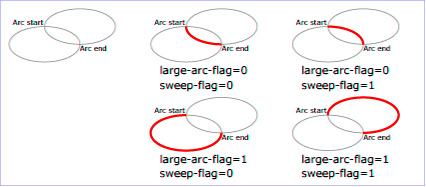
I hope this help is right. Please excuse my bad language. If you have some questions, I understand far better than I can be understood, but I can try to give you more informations.
Have a nice day!
Ollivier
Here is a code. You can use mouse wheel and drag the two blue points in the screen to check if it's good. You can check the flag box's at the top-left corner.
I didn't change more the code because it consists now in merging all the procedures. So, you couldn't understand easily the operations.
Thank to Michel Berteau site and particularly this page which allows me to create quickly the CircleEquation() procedure. (Note that there is small errors in the calculs at the end of the page, but I think it's willingly for the school cheaters to be betrayed if they copy foolishly. I don't think the author's wrong.)
@Seymour Clufley
You forgot a detail we can see here. In the global inventory, we need some flags the explanation could be well illustrated below (from official page).

I hope this help is right. Please excuse my bad language. If you have some questions, I understand far better than I can be understood, but I can try to give you more informations.
Have a nice day!
Ollivier
Code: Select all
Procedure.F GetOrientation(xCenter.F, yCenter.F, xSource.F, ySource.F)
Protected.F xDelta, yDelta
Protected.F Rho, Alpha
xDelta = xSource - xCenter
yDelta = ySource - yCenter
Rho = Sqr((xDelta * xDelta) + (yDelta * yDelta) )
Alpha = ACos(xDelta / Rho)
If yDelta > 0.
Alpha = - Alpha
EndIf
ProcedureReturn Alpha
EndProcedure
Procedure RotatePoint(xCenter.F, yCenter.F, xSource.F, ySource.F, Beta.F, *xResult, *yResult)
Protected.F xDelta1, yDelta1
Protected.F xRef, yRef
xDelta1 = xSource - xCenter
yDelta1 = ySource - yCenter
xRef = Cos(Beta)
yRef = Sin(Beta)
PokeF(*xResult, xCenter + xRef * xDelta1 + yRef * yDelta1)
PokeF(*yResult, yCenter - yRef * xDelta1 + xRef * yDelta1)
EndProcedure
Procedure ScalePoint(xCenter.F, yCenter.F, xScale.F, yScale.F, xSource.F, ySource.F, *xResult, *yResult)
PokeF(*xResult, (xSource - xCenter) * xScale + xCenter)
PokeF(*yResult, (ySource - yCenter) * yScale + yCenter)
EndProcedure
Procedure.I CircleEquation(x1.F, y1.F, x2.F, y2.F, R0.F, *px0, *py0, *pxE, *pyE)
Protected.I Result
Protected.F x1P2, y1P2, x2P2, y2P2, xDelta, yDelta, Dir
Protected.F N, A, B, C, Base, Root, x0, y0, xE, yE
Protected.I FlipFlag
If y1 = y2
Swap x1, y1
Swap x2, y2
FlipFlag = 1
EndIf
xDelta = x1 - x2
yDelta = y1 - y2
Dir = xDelta / yDelta
x1P2 = x1 * x1
y1P2 = y1 * y1
x2P2 = x2 * x2
y2P2 = y2 * y2
N = (x1P2 - x2P2 + y1P2 - y2P2) / (2. * yDelta)
A = (Dir * Dir) + 1.
B = 2. * ((y1 * Dir) - (N * Dir) - x1)
C = x1P2 + y1P2 + (N + R0) * (N - R0) - (2. * Y1 * N)
Delta = (B * B) - (4. * A * C)
If Delta => 0.
Base = - B / (2. * A)
Root = Sqr(Delta) / (2. * A)
x0 = Base - Root
y0 = N - (x0 * Dir)
xE = Base + Root
yE = N - (xE * Dir)
If FlipFlag
Swap x0, y0
Swap xE, yE
EndIf
PokeF(*px0, x0)
PokeF(*py0, y0)
PokeF(*pxE, xE)
PokeF(*pyE, yE)
Result = #True
Else
Result = #False
EndIf
ProcedureReturn Result
EndProcedure
Procedure.I GetArcChars(xStart.F, yStart.F, xEnd.F, yEnd.F, yRadius.F, xRadius.F, xRotation.F, LargeArcFlag.I, SweepFlag.I, *xResult1, *yResult1, *xResult2, *yResult2, *StartAngle, *EndAngle)
Protected.I Result
Protected.F xTemp, yTemp, xTmp, yTmp, xTmp0, yTmp0
Protected.F StartArc, EndArc, xA, yA, xB, yB, A1, A2, A3
RotatePoint(xStart, yStart, xEnd, yEnd, - xRotation, @xTemp, @yTemp)
ScalePoint(xStart, yStart, 1.0, yRadius / xRadius, xTemp, yTemp, @xTemp, @yTemp)
If CircleEquation(xStart, yStart, xTemp, yTemp, yRadius, @xTmp, @yTmp, @xTmp0, @yTmp0)
StartArc = GetOrientation(xTmp, yTmp, xStart, yStart)
EndArc = GetOrientation(xTmp, yTmp, xTemp, yTemp)
ScalePoint(xStart, yStart, 1.0, xRadius / yRadius, xTmp, yTmp, @xTmp, @yTmp)
ScalePoint(xStart, yStart, 1.0, xRadius / yRadius, xTmp0, yTmp0, @xTmp0, @yTmp0)
RotatePoint(xStart, yStart, xTmp, yTmp, xRotation, @xA, @yA)
RotatePoint(xStart, yStart, xTmp0, yTmp0, xRotation, @xB, @yB)
A1.F = GetOrientation(xStart, yStart, xA, yA) + #PI
A2.F = GetOrientation(xStart, yStart, xEnd, yEnd) + #PI
A3.F = GetOrientation(xStart, yStart, xB, yB) + #PI
If ((A1 > A2) And (A2 > A3) ) Or ((A1 < A2) And (A2 > A3) And (A1 < A3) ) Or ((A1 > A2) And (A2 < A3) And (A1 < A3) )
Swap xA, xB
Swap yA, yB
Swap StartArc, EndArc
StartArc + #PI
EndArc + #PI
EndIf
If LargeArcFlag = #False
Swap xA, xB
Swap yA, yB
Swap StartArc, EndArc
StartArc + #PI
EndArc + #PI
EndIf
If SweepFlag
Swap xA, xB
Swap yA, yB
StartArc + #PI
EndArc + #PI
EndIf
PokeF(*StartAngle, StartArc)
PokeF(*EndAngle, EndArc)
PokeF(*xResult1, xA)
PokeF(*yResult1, yA)
PokeF(*xResult2, xB)
PokeF(*yResult2, yB)
Result = #True
Else
Result = #False
EndIf
ProcedureReturn Result
EndProcedure
Procedure DrawArc(xCenter.F, yCenter.F, RadiusX.F, RadiusY.F, xRotation.F, Color.I, StartArc.F = 0., EndArc.F = 2. * #PI)
Protected.F AngleStep, Angle, xEllipse, yEllipse, xDraw, yDraw, xPlot, yPlot
AngleStep = #PI / (2. * (RadiusX + RadiusY) )
If EndArc < StartArc
EndArc + (2. * #PI)
EndIf
Angle = StartArc
Repeat
xEllipse.F = Cos(Angle) * RadiusX ;;
yEllipse.F = Sin(Angle) * RadiusY ;;
xDraw.F = Cos(xRotation) * xEllipse - Sin(xRotation) * yEllipse ;;
yDraw.F = - Sin(xRotation) * xEllipse - Cos(xRotation) * yEllipse ;;
xPlot.F = xCenter + xDraw
yPlot.F = yCenter + yDraw
Box(xPlot, yPlot, 1, 1, Color)
Angle + AngleStep
Until Angle > EndArc
EndProcedure
Procedure GetBoundArc(*Left.Float, *Top.Float, *Right.Float, *Bottom.Float, xCenter.F, yCenter.F, RadiusX.F, RadiusY.F, xRotation.F, StartArc.F = 0., EndArc.F = 2. * #PI)
Protected.F AngleStep, Angle, xEllipse, yEllipse, xDraw, yDraw, xPlot, yPlot
AngleStep = #PI / (2. * (RadiusX + RadiusY) )
If EndArc < StartArc
EndArc + (2. * #PI)
EndIf
Angle = StartArc
*Left\F = 9999999.
*Top\F = 9999999.
*Right\F = -9999999.
*Bottom\F = -9999999.
Repeat
xEllipse.F = Cos(Angle) * RadiusX ;;
yEllipse.F = Sin(Angle) * RadiusY ;;
xDraw.F = Cos(xRotation) * xEllipse - Sin(xRotation) * yEllipse ;;
yDraw.F = - Sin(xRotation) * xEllipse - Cos(xRotation) * yEllipse ;;
xPlot.F = xCenter + xDraw
yPlot.F = yCenter + yDraw
If xPlot < *Left\F
*Left\F = xPlot
EndIf
If xPlot > *Right\F
*Right\F = xPlot
EndIf
If yPlot < *Top\F
*Top\F = yPlot
EndIf
If yPLot > *Bottom\F
*Bottom\F = yPlot
EndIf
Angle + AngleStep
Until Angle > EndArc
EndProcedure
Define.F xA, yA, xB, yB, StartArc, EndArc
Define.I LargeArcFlag, SweepFlag
Define.F Left, Top, Right, Bottom
InitSprite()
InitKeyboard()
InitMouse()
ExamineDesktops()
dw = DesktopWidth(0)
dh = DesktopHeight(0)
dd = DesktopDepth(0)
OpenScreen(dw, dh, dd, "")
Global Dim x.F(1)
Global Dim y.F(1)
x(0) = dw / 2.
y(0) = dh / 2.
x(1) = x(0) + 30.
y(1) = y(0) + 30.
xRadius.F = Dw / 4.
yRadius.F = Dh / 8.
xRotation.F = 0.
GetArcChars(x(0), y(0), x(1), y(1), xRadius, yRadius, xRotation, LargeArcFlag, SweepFlag, @xA, @yA, @xB, @yB, @StartArc, @EndArc)
Modif = 1
Repeat
Delay(1)
ExamineKeyboard()
ExamineMouse()
Mw = MouseWheel()
Mx = MouseX()
My = MouseY()
Mdx = MouseDeltaX()
Mdy = MouseDeltaY()
Mb1 = MouseButton(1)
If Mw
Modif + (16 * Mw)
EndIf
If Modif > 0
xrotation + (#PI / 256.)
EndIf
If Modif < 0
xrotation - (#PI / 256.)
EndIf
If Mdx Or Mdy
Something = 0
For I = 0 To 1
Dx = x(I) - Mx
Dy = y(I) - My
If Sqr(Dx * Dx + Dy * Dy) < 5
Something = 1
ISet = I
EndIf
Next
If Something Or MoveIt
ChoseQuelle = 0
Else
ChoseQuelle = 16
EndIf
EndIf
If MB1
If Mx < 16
Choice = My / 16
If Change = 0
If Choice = 0
Modif | 1
Change = 1
LargeArcFlag ! 1
EndIf
If Choice = 1
Modif | 1
Change = 1
SweepFlag ! 1
EndIf
EndIf
EndIf
If Something
MoveIt = 1
EndIf
Else
Change = 0
MoveIt = 0
EndIf
If MoveIt Or Modif
If MoveIt
X(ISet) + Mdx
Y(ISet) + Mdy
EndIf
If Mdx Or Mdx Or Modif
DrawIsOk = GetArcChars(x(0), y(0), x(1), y(1), xRadius, yRadius, xRotation, LargeArcFlag, SweepFlag, @xA, @yA, @xB, @yB, @StartArc, @EndArc)
If Modif > 0
Modif - 1
EndIf
If Modif < 0
Modif + 1
EndIf
EndIf
EndIf
ClearScreen(RGB(255, 255, 255) )
StartDrawing(ScreenOutput() )
DrawingMode(#PB_2DDrawing_Transparent)
DrawText(16, 0, "Large-arc", RGB(0, 0, 0) )
DrawText(16, 16, "Sweep", RGB(0, 0, 0) )
Box(1, 1, 14, 14, RGB(0, 0, 0) )
If LargeArcFlag = 0
Box(3, 3, 10, 10, RGB(255, 255, 255) )
EndIf
Box(1, 1 + 16, 14, 14, RGB(0, 0, 0) )
If SweepFlag = 0
Box(3, 3 + 16, 10, 10, RGB(255, 255, 255) )
EndIf
If DrawIsOk
GetBoundArc(@Left, @Top, @Right, @Bottom, xA, yA, xRadius, yRadius, xRotation, StartArc, EndArc)
Box(Left, Top, Right - Left, Bottom - Top, RGB(230, 240, 255) )
Box(x(0) - 4, y(0) - 4, 9, 9, RGB(0, 0, 128) )
Box(x(1) - 4, y(1) - 4, 9, 9, RGB(0, 128, 255) )
DrawText(x(0) + 4, y(0) + 4, "Start", RGB(0, 0, 128) )
DrawText(x(1) + 4, y(1) + 4, "End", RGB(0, 128, 255) )
DrawArc(xA, yA, xRadius, yRadius, xRotation, RGB(200, 200, 200) )
DrawArc(xB, yB, xRadius, yRadius, xRotation, RGB(200, 200, 200) )
DrawArc(xA, yA, xRadius, yRadius, xRotation, RGB(255, 0, 0), StartArc, EndArc)
Else
DrawText(x(0) + 4, y(0) + 4, "Too far /!\", RGB(255, 0, 0) )
EndIf
Box(mx - 2, my - 2 - 10 - ChoseQuelle, 5, 5 + ChoseQuelle, RGB(0, 255, 0) )
Box(mx - 2, my - 2 + 10, 5, 5 + ChoseQuelle, RGB(0, 255, 0) )
Box(mx - 2 - 10 - ChoseQuelle, my - 2, 5 + ChoseQuelle, 5, RGB(0, 255, 0) )
Box(mx - 2 + 10, my - 2, 5 + ChoseQuelle, 5, RGB(0, 255, 0) )
StopDrawing()
FlipBuffers()
Until KeyboardPushed(#PB_Key_Escape)
CloseScreen()