Any maths gurus who can help with geometry?!
Re: Any maths gurus who can help with geometry?!
Yes the tangents to the x-/y-axis would do the job (following the rotation of the ellipse of course). I gave the actual horizontal/vertical bounds for a rotated ellipse centered at (0, 0) in a previous post, though I did not use tangents to determine them but good old trig. Determining the Cartesian bounds for an arc of such an ellipse is a little more involved.
I may look like a mule, but I'm not a complete ass.
Re: Any maths gurus who can help with geometry?!
Hello,
Here is a code. You can use mouse wheel and drag the two blue points in the screen to check if it's good. You can check the flag box's at the top-left corner.
I didn't change more the code because it consists now in merging all the procedures. So, you couldn't understand easily the operations.
Thank to Michel Berteau site and particularly this page which allows me to create quickly the CircleEquation() procedure. (Note that there is small errors in the calculs at the end of the page, but I think it's willingly for the school cheaters to be betrayed if they copy foolishly. I don't think the author's wrong.)
@Seymour Clufley
You forgot a detail we can see here. In the global inventory, we need some flags the explanation could be well illustrated below (from official page).
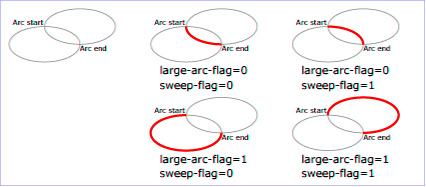
I hope this help is right. Please excuse my bad language. If you have some questions, I understand far better than I can be understood, but I can try to give you more informations.
Have a nice day!
Ollivier
Here is a code. You can use mouse wheel and drag the two blue points in the screen to check if it's good. You can check the flag box's at the top-left corner.
I didn't change more the code because it consists now in merging all the procedures. So, you couldn't understand easily the operations.
Thank to Michel Berteau site and particularly this page which allows me to create quickly the CircleEquation() procedure. (Note that there is small errors in the calculs at the end of the page, but I think it's willingly for the school cheaters to be betrayed if they copy foolishly. I don't think the author's wrong.)
@Seymour Clufley
You forgot a detail we can see here. In the global inventory, we need some flags the explanation could be well illustrated below (from official page).

I hope this help is right. Please excuse my bad language. If you have some questions, I understand far better than I can be understood, but I can try to give you more informations.
Have a nice day!
Ollivier
Code: Select all
Procedure.F GetOrientation(xCenter.F, yCenter.F, xSource.F, ySource.F)
Protected.F xDelta, yDelta
Protected.F Rho, Alpha
xDelta = xSource - xCenter
yDelta = ySource - yCenter
Rho = Sqr((xDelta * xDelta) + (yDelta * yDelta) )
Alpha = ACos(xDelta / Rho)
If yDelta > 0.
Alpha = - Alpha
EndIf
ProcedureReturn Alpha
EndProcedure
Procedure RotatePoint(xCenter.F, yCenter.F, xSource.F, ySource.F, Beta.F, *xResult, *yResult)
Protected.F xDelta1, yDelta1
Protected.F xRef, yRef
xDelta1 = xSource - xCenter
yDelta1 = ySource - yCenter
xRef = Cos(Beta)
yRef = Sin(Beta)
PokeF(*xResult, xCenter + xRef * xDelta1 + yRef * yDelta1)
PokeF(*yResult, yCenter - yRef * xDelta1 + xRef * yDelta1)
EndProcedure
Procedure ScalePoint(xCenter.F, yCenter.F, xScale.F, yScale.F, xSource.F, ySource.F, *xResult, *yResult)
PokeF(*xResult, (xSource - xCenter) * xScale + xCenter)
PokeF(*yResult, (ySource - yCenter) * yScale + yCenter)
EndProcedure
Procedure.I CircleEquation(x1.F, y1.F, x2.F, y2.F, R0.F, *px0, *py0, *pxE, *pyE)
Protected.I Result
Protected.F x1P2, y1P2, x2P2, y2P2, xDelta, yDelta, Dir
Protected.F N, A, B, C, Base, Root, x0, y0, xE, yE
Protected.I FlipFlag
If y1 = y2
Swap x1, y1
Swap x2, y2
FlipFlag = 1
EndIf
xDelta = x1 - x2
yDelta = y1 - y2
Dir = xDelta / yDelta
x1P2 = x1 * x1
y1P2 = y1 * y1
x2P2 = x2 * x2
y2P2 = y2 * y2
N = (x1P2 - x2P2 + y1P2 - y2P2) / (2. * yDelta)
A = (Dir * Dir) + 1.
B = 2. * ((y1 * Dir) - (N * Dir) - x1)
C = x1P2 + y1P2 + (N + R0) * (N - R0) - (2. * Y1 * N)
Delta = (B * B) - (4. * A * C)
If Delta => 0.
Base = - B / (2. * A)
Root = Sqr(Delta) / (2. * A)
x0 = Base - Root
y0 = N - (x0 * Dir)
xE = Base + Root
yE = N - (xE * Dir)
If FlipFlag
Swap x0, y0
Swap xE, yE
EndIf
PokeF(*px0, x0)
PokeF(*py0, y0)
PokeF(*pxE, xE)
PokeF(*pyE, yE)
Result = #True
Else
Result = #False
EndIf
ProcedureReturn Result
EndProcedure
Procedure.I GetArcChars(xStart.F, yStart.F, xEnd.F, yEnd.F, yRadius.F, xRadius.F, xRotation.F, LargeArcFlag.I, SweepFlag.I, *xResult1, *yResult1, *xResult2, *yResult2, *StartAngle, *EndAngle)
Protected.I Result
Protected.F xTemp, yTemp, xTmp, yTmp, xTmp0, yTmp0
Protected.F StartArc, EndArc, xA, yA, xB, yB, A1, A2, A3
RotatePoint(xStart, yStart, xEnd, yEnd, - xRotation, @xTemp, @yTemp)
ScalePoint(xStart, yStart, 1.0, yRadius / xRadius, xTemp, yTemp, @xTemp, @yTemp)
If CircleEquation(xStart, yStart, xTemp, yTemp, yRadius, @xTmp, @yTmp, @xTmp0, @yTmp0)
StartArc = GetOrientation(xTmp, yTmp, xStart, yStart)
EndArc = GetOrientation(xTmp, yTmp, xTemp, yTemp)
ScalePoint(xStart, yStart, 1.0, xRadius / yRadius, xTmp, yTmp, @xTmp, @yTmp)
ScalePoint(xStart, yStart, 1.0, xRadius / yRadius, xTmp0, yTmp0, @xTmp0, @yTmp0)
RotatePoint(xStart, yStart, xTmp, yTmp, xRotation, @xA, @yA)
RotatePoint(xStart, yStart, xTmp0, yTmp0, xRotation, @xB, @yB)
A1.F = GetOrientation(xStart, yStart, xA, yA) + #PI
A2.F = GetOrientation(xStart, yStart, xEnd, yEnd) + #PI
A3.F = GetOrientation(xStart, yStart, xB, yB) + #PI
If ((A1 > A2) And (A2 > A3) ) Or ((A1 < A2) And (A2 > A3) And (A1 < A3) ) Or ((A1 > A2) And (A2 < A3) And (A1 < A3) )
Swap xA, xB
Swap yA, yB
Swap StartArc, EndArc
StartArc + #PI
EndArc + #PI
EndIf
If LargeArcFlag = #False
Swap xA, xB
Swap yA, yB
Swap StartArc, EndArc
StartArc + #PI
EndArc + #PI
EndIf
If SweepFlag
Swap xA, xB
Swap yA, yB
StartArc + #PI
EndArc + #PI
EndIf
PokeF(*StartAngle, StartArc)
PokeF(*EndAngle, EndArc)
PokeF(*xResult1, xA)
PokeF(*yResult1, yA)
PokeF(*xResult2, xB)
PokeF(*yResult2, yB)
Result = #True
Else
Result = #False
EndIf
ProcedureReturn Result
EndProcedure
Procedure DrawArc(xCenter.F, yCenter.F, RadiusX.F, RadiusY.F, xRotation.F, Color.I, StartArc.F = 0., EndArc.F = 2. * #PI)
Protected.F AngleStep, Angle, xEllipse, yEllipse, xDraw, yDraw, xPlot, yPlot
AngleStep = #PI / (2. * (RadiusX + RadiusY) )
If EndArc < StartArc
EndArc + (2. * #PI)
EndIf
Angle = StartArc
Repeat
xEllipse.F = Cos(Angle) * RadiusX ;;
yEllipse.F = Sin(Angle) * RadiusY ;;
xDraw.F = Cos(xRotation) * xEllipse - Sin(xRotation) * yEllipse ;;
yDraw.F = - Sin(xRotation) * xEllipse - Cos(xRotation) * yEllipse ;;
xPlot.F = xCenter + xDraw
yPlot.F = yCenter + yDraw
Box(xPlot, yPlot, 1, 1, Color)
Angle + AngleStep
Until Angle > EndArc
EndProcedure
Procedure GetBoundArc(*Left.Float, *Top.Float, *Right.Float, *Bottom.Float, xCenter.F, yCenter.F, RadiusX.F, RadiusY.F, xRotation.F, StartArc.F = 0., EndArc.F = 2. * #PI)
Protected.F AngleStep, Angle, xEllipse, yEllipse, xDraw, yDraw, xPlot, yPlot
AngleStep = #PI / (2. * (RadiusX + RadiusY) )
If EndArc < StartArc
EndArc + (2. * #PI)
EndIf
Angle = StartArc
*Left\F = 9999999.
*Top\F = 9999999.
*Right\F = -9999999.
*Bottom\F = -9999999.
Repeat
xEllipse.F = Cos(Angle) * RadiusX ;;
yEllipse.F = Sin(Angle) * RadiusY ;;
xDraw.F = Cos(xRotation) * xEllipse - Sin(xRotation) * yEllipse ;;
yDraw.F = - Sin(xRotation) * xEllipse - Cos(xRotation) * yEllipse ;;
xPlot.F = xCenter + xDraw
yPlot.F = yCenter + yDraw
If xPlot < *Left\F
*Left\F = xPlot
EndIf
If xPlot > *Right\F
*Right\F = xPlot
EndIf
If yPlot < *Top\F
*Top\F = yPlot
EndIf
If yPLot > *Bottom\F
*Bottom\F = yPlot
EndIf
Angle + AngleStep
Until Angle > EndArc
EndProcedure
Define.F xA, yA, xB, yB, StartArc, EndArc
Define.I LargeArcFlag, SweepFlag
Define.F Left, Top, Right, Bottom
InitSprite()
InitKeyboard()
InitMouse()
ExamineDesktops()
dw = DesktopWidth(0)
dh = DesktopHeight(0)
dd = DesktopDepth(0)
OpenScreen(dw, dh, dd, "")
Global Dim x.F(1)
Global Dim y.F(1)
x(0) = dw / 2.
y(0) = dh / 2.
x(1) = x(0) + 30.
y(1) = y(0) + 30.
xRadius.F = Dw / 4.
yRadius.F = Dh / 8.
xRotation.F = 0.
GetArcChars(x(0), y(0), x(1), y(1), xRadius, yRadius, xRotation, LargeArcFlag, SweepFlag, @xA, @yA, @xB, @yB, @StartArc, @EndArc)
Modif = 1
Repeat
Delay(1)
ExamineKeyboard()
ExamineMouse()
Mw = MouseWheel()
Mx = MouseX()
My = MouseY()
Mdx = MouseDeltaX()
Mdy = MouseDeltaY()
Mb1 = MouseButton(1)
If Mw
Modif + (16 * Mw)
EndIf
If Modif > 0
xrotation + (#PI / 256.)
EndIf
If Modif < 0
xrotation - (#PI / 256.)
EndIf
If Mdx Or Mdy
Something = 0
For I = 0 To 1
Dx = x(I) - Mx
Dy = y(I) - My
If Sqr(Dx * Dx + Dy * Dy) < 5
Something = 1
ISet = I
EndIf
Next
If Something Or MoveIt
ChoseQuelle = 0
Else
ChoseQuelle = 16
EndIf
EndIf
If MB1
If Mx < 16
Choice = My / 16
If Change = 0
If Choice = 0
Modif | 1
Change = 1
LargeArcFlag ! 1
EndIf
If Choice = 1
Modif | 1
Change = 1
SweepFlag ! 1
EndIf
EndIf
EndIf
If Something
MoveIt = 1
EndIf
Else
Change = 0
MoveIt = 0
EndIf
If MoveIt Or Modif
If MoveIt
X(ISet) + Mdx
Y(ISet) + Mdy
EndIf
If Mdx Or Mdx Or Modif
DrawIsOk = GetArcChars(x(0), y(0), x(1), y(1), xRadius, yRadius, xRotation, LargeArcFlag, SweepFlag, @xA, @yA, @xB, @yB, @StartArc, @EndArc)
If Modif > 0
Modif - 1
EndIf
If Modif < 0
Modif + 1
EndIf
EndIf
EndIf
ClearScreen(RGB(255, 255, 255) )
StartDrawing(ScreenOutput() )
DrawingMode(#PB_2DDrawing_Transparent)
DrawText(16, 0, "Large-arc", RGB(0, 0, 0) )
DrawText(16, 16, "Sweep", RGB(0, 0, 0) )
Box(1, 1, 14, 14, RGB(0, 0, 0) )
If LargeArcFlag = 0
Box(3, 3, 10, 10, RGB(255, 255, 255) )
EndIf
Box(1, 1 + 16, 14, 14, RGB(0, 0, 0) )
If SweepFlag = 0
Box(3, 3 + 16, 10, 10, RGB(255, 255, 255) )
EndIf
If DrawIsOk
GetBoundArc(@Left, @Top, @Right, @Bottom, xA, yA, xRadius, yRadius, xRotation, StartArc, EndArc)
Box(Left, Top, Right - Left, Bottom - Top, RGB(230, 240, 255) )
Box(x(0) - 4, y(0) - 4, 9, 9, RGB(0, 0, 128) )
Box(x(1) - 4, y(1) - 4, 9, 9, RGB(0, 128, 255) )
DrawText(x(0) + 4, y(0) + 4, "Start", RGB(0, 0, 128) )
DrawText(x(1) + 4, y(1) + 4, "End", RGB(0, 128, 255) )
DrawArc(xA, yA, xRadius, yRadius, xRotation, RGB(200, 200, 200) )
DrawArc(xB, yB, xRadius, yRadius, xRotation, RGB(200, 200, 200) )
DrawArc(xA, yA, xRadius, yRadius, xRotation, RGB(255, 0, 0), StartArc, EndArc)
Else
DrawText(x(0) + 4, y(0) + 4, "Too far /!\", RGB(255, 0, 0) )
EndIf
Box(mx - 2, my - 2 - 10 - ChoseQuelle, 5, 5 + ChoseQuelle, RGB(0, 255, 0) )
Box(mx - 2, my - 2 + 10, 5, 5 + ChoseQuelle, RGB(0, 255, 0) )
Box(mx - 2 - 10 - ChoseQuelle, my - 2, 5 + ChoseQuelle, 5, RGB(0, 255, 0) )
Box(mx - 2 + 10, my - 2, 5 + ChoseQuelle, 5, RGB(0, 255, 0) )
StopDrawing()
FlipBuffers()
Until KeyboardPushed(#PB_Key_Escape)
CloseScreen()
Re: Any maths gurus who can help with geometry?!
Very very nice. 
Now what about ellipses which are rotated?
Now what about ellipses which are rotated?
I may look like a mule, but I'm not a complete ass.
Re: Any maths gurus who can help with geometry?!
@Stephen
Hello! If you would use your mouse wheel, would not be there better?
Ollivier
Hello! If you would use your mouse wheel, would not be there better?
Ollivier
Re: Any maths gurus who can help with geometry?!
@Stephen
I'll try to be more precise!
Line 202 : record the stat of the mouse wheel in the integer variable Mw (MouseWheel)
Line 208-210 : Multiply the mouse wheel action by 16 and store the result in the integer value Modif (Modification)
Line 256 : This condition is also true because Modif is non zero...
Line 261 : ...And this condition is true again...
Line 262 : ...so, execute the most interesting procedure of the code...
Line 263-268 : Decrease or increase (in accordance with the sign, positive or negative of the variable) the variable Modif to go to zero.
Conclusion : A little rotation of the mouse wheel causes 16 rotations of the ellipses at the screen!
In this text, I said this following line contained the most intersting procedure in the code:
It's evident. First, the name GetArcChars() = Get Arc Characteristics.
You give it informations and this procedure gives you others informations.
In reality, this procedure gives you the two centers of each possible ellipse AND it gives you too the angles (in radian) mini and maxi of you arc.
The manner to receive informations from this (and the others procedure in this code) procedure consists in giving it the pointor of the float variable which will contain the future result after the execution of the procedure.
The result (here it's DrawIsOk variable) is true if the informations given let's suppose it exists two ellipses which touch the two points given. If the two points are too far or if the ellipses are too small, there isn't solution, so the result will be false.
Finally, the informations you must give to this procedure are exactly the same as the ones are here. All these informations, and only these informations!
We can see we must give the angle (xRotation.F) in the input arguments.
(Note that all these procedures can be directly compiled in a DLL file. Logically, these procedures shouldn't crash in other OS (Linux and Mac) )
Have a nice day!
Ollivier
I'll try to be more precise!
Thank you !!!srod wrote:Very very nice.
In the code above, you can see this:srod wrote:Now what about ellipses which are rotated?
Line 202 : record the stat of the mouse wheel in the integer variable Mw (MouseWheel)
Code: Select all
Mw = MouseWheel()Code: Select all
If Mw
Modif + (16 * Mw)
EndIfCode: Select all
If MoveIt Or ModifCode: Select all
If Mdx Or Mdx Or ModifCode: Select all
DrawIsOk = GetArcChars(x(0), y(0), x(1), y(1), xRadius, yRadius, xRotation, LargeArcFlag, SweepFlag, @xA, @yA, @xB, @yB, @StartArc, @EndArc)Code: Select all
If Modif > 0
Modif - 1
EndIf
If Modif < 0
Modif + 1
EndIfIn this text, I said this following line contained the most intersting procedure in the code:
Code: Select all
DrawIsOk = GetArcChars(x(0), y(0), x(1), y(1), xRadius, yRadius, xRotation, LargeArcFlag, SweepFlag, @xA, @yA, @xB, @yB, @StartArc, @EndArc)You give it informations and this procedure gives you others informations.
In reality, this procedure gives you the two centers of each possible ellipse AND it gives you too the angles (in radian) mini and maxi of you arc.
The manner to receive informations from this (and the others procedure in this code) procedure consists in giving it the pointor of the float variable which will contain the future result after the execution of the procedure.
The result (here it's DrawIsOk variable) is true if the informations given let's suppose it exists two ellipses which touch the two points given. If the two points are too far or if the ellipses are too small, there isn't solution, so the result will be false.
Finally, the informations you must give to this procedure are exactly the same as the ones are here. All these informations, and only these informations!
We can see we must give the angle (xRotation.F) in the input arguments.
(Note that all these procedures can be directly compiled in a DLL file. Logically, these procedures shouldn't crash in other OS (Linux and Mac) )
Have a nice day!
Ollivier
Re: Any maths gurus who can help with geometry?!
Ups excuse me... :roll:srod wrote:Now what about ellipses which are rotated?
In the "mathematical sense" it's possible but "useless".
The process of the procedure GetArcChars() is: (what we can see in the code above)
1) Rotation to get a "right" or "non-rotated" virtual ellipse
2) Deformation to change from the virtual ellipse to a virtual circle
3) Get real circle equation from the two points (which have been changed in (1) and (2) ) and the radius. Result are two circle centers
4) "back" deformation to change from circles centers to ellipses centers
5) "back" rotation to change from "non-rotated" ellipses centers to rotated ellipses centers.
If you want to calculate directly the two points (delete 1,2, 4 and 5 steps) you will get a very big calcul of Golgot... I said it's useless because it's equivalent to give this
a² + b² + 2.a.b (or a² + 2.a.b + b²)
instead of this:
(a + b)²
The second process is more quickly executed than the first process.
The advantage to have a single very big mathematical calculus is in the way you have others goals more complex than only get bounds of an arc...
This choice is a compromise between speed and coding flexibility, but you're right it doesn't mean it is the best choice!
Re: Any maths gurus who can help with geometry?!
in case this may still be useful
Code: Select all
Procedure DrawArc(color.i,ptx,pty,majoraxis.f,minoraxis.f,orient.f,start.f,finish.f)
Protected hdc,cx.f,cy.f,dx.f,dy.f,ndx,ndy,r1.rect,da
Protected theta.f,dx1.f,dy1.f,cosOrient.f,SinOrient.f
hdc = StartDrawing(WindowOutput(0))
cx = ptx
cy = pty
cosOrient = Cos(orient)
sinOrient = Sin(orient)
If start < finish
sta = start
eta = finish
Else
sta = finish
eta = start
EndIf
xs = 800
xt = 0
ys = 600
yt = 0
;draw a rough elipse
For da = sta To eta
theta = da * (#PI/180.0)
dx = cx + (Sin(theta) * majoraxis)
dy = cy + (Cos(theta) * minoraxis)
dx1 = dx - cx
dy1 = dy - cy
ndx = cx + (dx1 * sinOrient - dy1 * cosorient) ;rotate elipse
ndy = cy + (dx1 * cosOrient + dy1 * sinorient)
If Not snx
snx = ndx
sny = ndy
EndIf
If da = eta
snx1 = ndx
sny1 = ndy
EndIf
If ndx > 0 And ndx < 800 And ndy > 0 And ndy < 600
Plot(ndx, ndy,~color & $FFFF)
If ndx > xt
xt = ndx
EndIf
If ndx < xs
xs = ndx
EndIf
If ndy > yt
yt = ndy
EndIf
If ndy < ys
ys = ndy
EndIf
EndIf
Next
LineXY(xs,ys,xt,ys,#Red)
LineXY(xs,ys,xs,yt,#Red)
LineXY(xs,yt,xt,yt,#Red)
LineXY(xt,yt,xt,ys,#Red)
LineXY(cx,cy,snx,sny,#Blue)
LineXY(cx,cy,snx1,sny1,#Blue)
Plot(Int(cx),Int(cy), color)
StopDrawing()
EndProcedure
Global pt.point
RandomSeed(timeGetTime_())
OpenWindow(0,0,0,800,600,"",#PB_Window_ScreenCentered | #PB_Window_SystemMenu )
Repeat
ev = WaitWindowEvent()
If ev = #WM_LBUTTONUP
pt\x=WindowMouseX(0)
pt\y=WindowMouseY(0)
DrawArc(RGB(255,0,0),pt\x,pt\y,Random(100)+1, Random(100)+1,Random(359)+1,Random(329)+30,Random(329)+30)
EndIf
Until ev = #PB_Event_CloseWindow
Last edited by idle on Sat Jan 23, 2010 11:24 am, edited 1 time in total.
Re: Any maths gurus who can help with geometry?!
@Idle
In the code I give above, we can see it:Etc... And I gave code and help about it here. 
It's more old than two years ago :roll:
I think what is now usefull is watching the reaction of Seymour Clufley when he will discover all the solution is now ready in one lonely code above!
I think the next step will consist in a good and comprehensive explanation of this code if you want. Algo illustration and maybe an explication of this famous math page.
In the code I give above, we can see it:
Code: Select all
Procedure DrawArc(xCenter.F, yCenter.F, RadiusX.F, RadiusY.F, xRotation.F, Color.I, StartArc.F = 0., EndArc.F = 2. * #PI)It's more old than two years ago :roll:
I think what is now usefull is watching the reaction of Seymour Clufley when he will discover all the solution is now ready in one lonely code above!
I think the next step will consist in a good and comprehensive explanation of this code if you want. Algo illustration and maybe an explication of this famous math page.
Re: Any maths gurus who can help with geometry?!
@Olliv
your solution is very good plus it answers the question of the bounding box.
I just altered what I posted earlier as I hadn't had the time to do anything about it.
your solution is very good plus it answers the question of the bounding box.
I just altered what I posted earlier as I hadn't had the time to do anything about it.
Re: Any maths gurus who can help with geometry?!
@Idle
As I don't know actually and exactly why and how does Seymour Clufley use his algo (using frequency, displaying or not displaying), I ignore if the preference of sRod is important or not...
Ollivier
Thank you.Idle wrote:your solution is very good plus it answers the question of the bounding box.
That's right I didn't enter in the discussion. That's my problem: I must translate and sometimes I can't enter in a good discussion. The problem that it causes actually is you and I are using a particular algo to get the bounds of an arc. And Stephen (sRod) is more intersted with an other algo which would be more "mathematic". In the way there is lots of arc to calculate and this is not necessary to display thelm, his algo should be normally quicker...Idle wrote:I just altered what I posted earlier as I hadn't had the time to do anything about it.
As I don't know actually and exactly why and how does Seymour Clufley use his algo (using frequency, displaying or not displaying), I ignore if the preference of sRod is important or not...
Ollivier
Re: Any maths gurus who can help with geometry?!
@Olliv : ... my apologies, I didn't use the mouse-wheel! Doh! 
Outstanding work! Brilliant.
Outstanding work! Brilliant.
I may look like a mule, but I'm not a complete ass.
-
Seymour Clufley
- Addict

- Posts: 1267
- Joined: Wed Feb 28, 2007 9:13 am
- Location: London
Re: Any maths gurus who can help with geometry?!
Well thankyou very much, Olivier and Idle, for working on this for me.
Unfortunately I can't test it yet because I'm not at home (not on forum much), but I will test it ASAP.
Thanks again for this code. You've both been very helpful!
Seymour.
Unfortunately I can't test it yet because I'm not at home (not on forum much), but I will test it ASAP.
Thanks again for this code. You've both been very helpful!
Seymour.
JACK WEBB: "Coding in C is like sculpting a statue using only sandpaper. You can do it, but the result wouldn't be any better. So why bother? Just use the right tools and get the job done."
Re: Any maths gurus who can help with geometry?!
your welcome, though the thanks should really go to Olliv as he has actually done the SVG implementation.
Re: Any maths gurus who can help with geometry?!
Ok, I give explications for each procedures and step by step, in the way there is some questions or remarks (if there is a bug or language error for example)
Name : GetOrientation()
Action : Get the absolute orientation between the segment going through the two given points and the horizontal line (or x-axis). An angle which turn at left is considered positive (like trigo norm).
Inputs :
xCenter.F ; yCenter.F First point position
xSource.F ; ySource.F Second point position
Output :
Return value (float) give the orientation (in radians).
Example :
Debug GetOrientation(0, 0, 1, 0)
The center is at 0, 0 and the second point is at 1, 0. So, the segment will be horizontal. The result is zero.
0.000
Debug GetOrientation(1, 1, 1, 2) / #PI
The center is at 1, 1 and the second point is at 1, 2. So, the segment will be vertical. The result is Pi/2 :
-0.500
Note: The result of the second example is negative because the procedure calculates exactly like a math referentiel when to go up increases the y value. (The screen referentiel decreases the y value when we go up on it)
Name : GetOrientation()
Action : Get the absolute orientation between the segment going through the two given points and the horizontal line (or x-axis). An angle which turn at left is considered positive (like trigo norm).
Inputs :
xCenter.F ; yCenter.F First point position
xSource.F ; ySource.F Second point position
Output :
Return value (float) give the orientation (in radians).
Example :
Debug GetOrientation(0, 0, 1, 0)
The center is at 0, 0 and the second point is at 1, 0. So, the segment will be horizontal. The result is zero.
0.000
Debug GetOrientation(1, 1, 1, 2) / #PI
The center is at 1, 1 and the second point is at 1, 2. So, the segment will be vertical. The result is Pi/2 :
-0.500
Note: The result of the second example is negative because the procedure calculates exactly like a math referentiel when to go up increases the y value. (The screen referentiel decreases the y value when we go up on it)
Code: Select all
Procedure.F GetOrientation(xCenter.F, yCenter.F, xSource.F, ySource.F)
Protected.F xDelta, yDelta
Protected.F Rho, Alpha
xDelta = xSource - xCenter
yDelta = ySource - yCenter
Rho = Sqr((xDelta * xDelta) + (yDelta * yDelta) )
Alpha = ACos(xDelta / Rho)
If yDelta > 0.
Alpha = - Alpha
EndIf
ProcedureReturn Alpha
EndProcedureRe: Any maths gurus who can help with geometry?!
Name : RotatePoint()
Action : Rotate a source point around a center point with a angle named beta. The new got point is stored in the "result" point.
Inputs :
xCenter.F ; yCenter.F Center point position (in pixels)
xSource.F ; ySource.F Source point position (in pixels)
Beta.F Rotation angle (in radians)
*xResult.FLOAT, *yResult.FLOAT Result point pointors
Output :
xResult.F, yResult.F Result point position
Example :
Define.F x, y
RotatePoint(1., 1., 2., 1., #PI / 2., @x, @y)
Debug x
Debug y
Will display near 1. and near 0.
Note: The rotation norm is different there. It's in accordance with the screen referentiel: increase the angle value is turn right.
Action : Rotate a source point around a center point with a angle named beta. The new got point is stored in the "result" point.
Inputs :
xCenter.F ; yCenter.F Center point position (in pixels)
xSource.F ; ySource.F Source point position (in pixels)
Beta.F Rotation angle (in radians)
*xResult.FLOAT, *yResult.FLOAT Result point pointors
Output :
xResult.F, yResult.F Result point position
Example :
Define.F x, y
RotatePoint(1., 1., 2., 1., #PI / 2., @x, @y)
Debug x
Debug y
Will display near 1. and near 0.
Note: The rotation norm is different there. It's in accordance with the screen referentiel: increase the angle value is turn right.
Code: Select all
Procedure RotatePoint(xCenter.F, yCenter.F, xSource.F, ySource.F, Beta.F, *xResult.FLOAT, *yResult.FLOAT)
Protected.F xDelta1, yDelta1
Protected.F xRef, yRef
xDelta1 = xSource - xCenter
yDelta1 = ySource - yCenter
xRef = Cos(Beta)
yRef = Sin(Beta)
*xResult\F = xCenter + xRef * xDelta1 + yRef * yDelta1
*yResult\F = yCenter - yRef * xDelta1 + xRef * yDelta1
EndProcedure

